Lösung 4.2:4e
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 7: | Zeile 7: | ||
[[Image:4_2_4_e1.gif|center]] | [[Image:4_2_4_e1.gif|center]] | ||
| - | <math>\tan (7\pi/6)</math> ist die Steigung der Geraden mit dem Winkel <math>7\pi/6</math>. | + | <math>\tan (7\pi/6)</math> ist die Steigung der Geraden mit dem Winkel <math>7\pi/6</math>. Da die Gerade mit dem Winkel <math>\pi/6</math> dieselbe Steigung hat, erhalten wir |
{{Abgesetzte Formel||<math>\tan\frac{7\pi}{6} = \tan\frac{\pi}{6} = \frac{\sin\dfrac{\pi }{6}}{\cos\dfrac{\pi }{6}} = \frac{\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>\tan\frac{7\pi}{6} = \tan\frac{\pi}{6} = \frac{\sin\dfrac{\pi }{6}}{\cos\dfrac{\pi }{6}} = \frac{\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}}\,\textrm{.}</math>}} | ||
[[Image:4_2_4_e2.gif|center]] | [[Image:4_2_4_e2.gif|center]] | ||
Version vom 17:21, 23. Jul. 2009
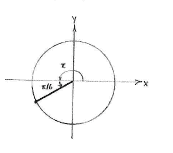
Wir schreiben \displaystyle \frac{7\pi}{6} als
| \displaystyle \frac{7\pi}{6} = \frac{6\pi+\pi}{6} = \pi + \frac{\pi }{6} |
und sehen, dass \displaystyle 7\pi/6 im dritten Quadrant liegt und damit den negativen Winkel \displaystyle \pi/6 zur x-Achse bildet.
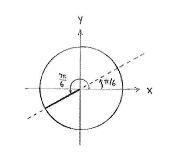
\displaystyle \tan (7\pi/6) ist die Steigung der Geraden mit dem Winkel \displaystyle 7\pi/6. Da die Gerade mit dem Winkel \displaystyle \pi/6 dieselbe Steigung hat, erhalten wir
| \displaystyle \tan\frac{7\pi}{6} = \tan\frac{\pi}{6} = \frac{\sin\dfrac{\pi }{6}}{\cos\dfrac{\pi }{6}} = \frac{\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}}\,\textrm{.} |