Lösung 4.4:3d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 7: | Zeile 7: | ||
Also ist die allgemeine Lösung | Also ist die allgemeine Lösung | ||
| - | {{Abgesetzte Formel||<math>3x = 15^{\circ} + n\cdot 360^{\circ}\qquad\text{und}\qquad 3x = 165^{\circ} + n\cdot 360^{\circ}\, | + | {{Abgesetzte Formel||<math>3x = 15^{\circ} + n\cdot 360^{\circ}\qquad\text{und}\qquad 3x = 165^{\circ} + n\cdot 360^{\circ}\,.</math>}} |
| - | + | Wir haben damit die Lösung | |
{{Abgesetzte Formel||<math>x = 5^{\circ} + n\cdot 120^{\circ}\qquad\text{und}\qquad x = 55^{\circ} + n\cdot 120^{\circ}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>x = 5^{\circ} + n\cdot 120^{\circ}\qquad\text{und}\qquad x = 55^{\circ} + n\cdot 120^{\circ}\,\textrm{.}</math>}} | ||
Version vom 14:27, 19. Jun. 2009
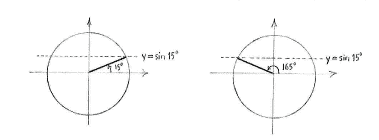
Wir erhalten zwei Lösungen im Intervall \displaystyle 0^{\circ}\le 3x\le 360^{\circ}\,,
| \displaystyle 3x = 15^{\circ}\qquad\text{und}\qquad 3x = 180^{\circ} - 15^{\circ} = 165^{\circ}\,\textrm{.} |
Also ist die allgemeine Lösung
| \displaystyle 3x = 15^{\circ} + n\cdot 360^{\circ}\qquad\text{und}\qquad 3x = 165^{\circ} + n\cdot 360^{\circ}\,. |
Wir haben damit die Lösung
| \displaystyle x = 5^{\circ} + n\cdot 120^{\circ}\qquad\text{und}\qquad x = 55^{\circ} + n\cdot 120^{\circ}\,\textrm{.} |