Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Lösung 4.4:2c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
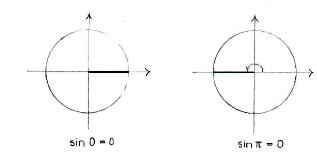
Es gibt zwei Winkeln am Einheitskreis die den Sinus null haben, nämlich <math>x=0</math> und <math>x=\pi</math>.
+
Es gibt zwei Winkel am Einheitskreis die den Sinus Null haben, nämlich <math>x=0</math> und <math>x=\pi</math>.
[[Image:4_4_2_c.gif|center]]
[[Image:4_4_2_c.gif|center]]
-
Addieren wir einen Multipel von <math>2\pi</math> zu diesen Winkeln erhalten wir die allgemeine Lösung,
+
Addieren wir einen Vielfaches von <math>2\pi</math> zu diesen Winkeln, erhalten wir die allgemeine Lösung,
{{Abgesetzte Formel||<math>x = 0+2n\pi\qquad\text{and}\qquad x = \pi + 2n\pi\,,</math>}}
{{Abgesetzte Formel||<math>x = 0+2n\pi\qquad\text{and}\qquad x = \pi + 2n\pi\,,</math>}}

Version vom 14:18, 19. Jun. 2009

Es gibt zwei Winkel am Einheitskreis die den Sinus Null haben, nämlich x=0 und x=.

Addieren wir einen Vielfaches von 2 zu diesen Winkeln, erhalten wir die allgemeine Lösung,

x=0+2nandx=+2n

Hinweis: Nachdem der Unterschied zwischen den beiden Lösungen im Einheitskreis genau ist, kann die Lösung kompakter geschrieben werden:

x=0+n
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:2c“