Lösung 4.3:5
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
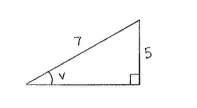
| - | Nachdem ''v'' ein | + | Nachdem ''v'' ein spitzer Winkel ist, können wir diesen in ein rechtwinkliges Dreieck einzeichnen, wo <math>\sin v = 5/7\,</math>. |
[[Image:4_3_5_1.gif|center]] | [[Image:4_3_5_1.gif|center]] | ||
| - | + | Durch den Satz des Pythagoras erhalten wir die Länge der unbekannten Seite des Dreiecks: | |
{| align="center" | {| align="center" | ||
Version vom 12:40, 19. Jun. 2009
Nachdem v ein spitzer Winkel ist, können wir diesen in ein rechtwinkliges Dreieck einzeichnen, wo \displaystyle \sin v = 5/7\,.
Durch den Satz des Pythagoras erhalten wir die Länge der unbekannten Seite des Dreiecks:
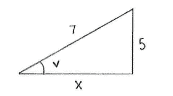
| \displaystyle \begin{align}&x^2 + 5^2 = 7^2\\[5pt] &\text{und wir erhalten}\\[5pt] &x = \sqrt{7^2-5^2} = \sqrt{24} = 2\sqrt{6}\end{align} |
Durch die Definitionen von Kosinus und Tangens erhalten wir
| \displaystyle \begin{align}
\cos v &= \frac{x}{7} = \frac{2\sqrt{6}}{7}\,,\\[5pt] \tan v &= \frac{5}{x} = \frac{5}{2\sqrt{6}}\,\textrm{.} \end{align} |