Lösung 4.2:9
Aus Online Mathematik Brückenkurs 1
(Sprache und Formulierung) |
|||
| Zeile 1: | Zeile 1: | ||
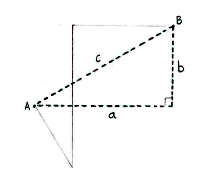
| - | Wir betrachten das Dreieck im unteren Bild. Der | + | Wir betrachten das Dreieck im unteren Bild. Der gesuchte Abstand ist die Hypotenuse ''c''. |
[[Image:4_2_9_1.gif|center]] | [[Image:4_2_9_1.gif|center]] | ||
| - | Die Hypotenuse können wir durch | + | Die Hypotenuse können wir durch den Satz des Pythagoras bestimmen |
{{Abgesetzte Formel||<math>c^2 = a^2 + b^2\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>c^2 = a^2 + b^2\,\textrm{.}</math>}} | ||
| Zeile 11: | Zeile 11: | ||
[[Image:4_2_9_2.gif|center]] | [[Image:4_2_9_2.gif|center]] | ||
| - | Nachdem <math>\text{AP}=4</math> erhalten wir einfach ''x'' und ''y'' | + | Nachdem <math>\text{AP}=4</math>, erhalten wir einfach ''x'' und ''y'': |
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
| Zeile 18: | Zeile 18: | ||
\end{align}</math>}} | \end{align}</math>}} | ||
| - | Mit ''x'' und ''y'' erhalten wir die Katheten ''a'' und ''b'' indem wir die horizontalen und vertikalen Abstände in der Figur betrachten. | + | Mit ''x'' und ''y'' erhalten wir die Katheten ''a'' und ''b'', indem wir die horizontalen und vertikalen Abstände in der Figur betrachten. |
{| align="center" | {| align="center" | ||
| Zeile 30: | Zeile 30: | ||
|} | |} | ||
| - | Mit ''a'' und ''b'' erhalten wir c durch | + | Mit ''a'' und ''b'' erhalten wir c durch den Satz des Pythagoras |
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
Version vom 13:34, 18. Jun. 2009
Wir betrachten das Dreieck im unteren Bild. Der gesuchte Abstand ist die Hypotenuse c.
Die Hypotenuse können wir durch den Satz des Pythagoras bestimmen
| \displaystyle c^2 = a^2 + b^2\,\textrm{.} |
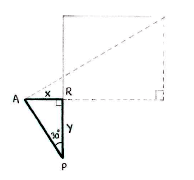
Wir können die Katheten bestimmen, indem wir das Dreieck APR im nächsten Bild betrachten.
Nachdem \displaystyle \text{AP}=4, erhalten wir einfach x und y:
| \displaystyle \begin{align}
x &= 4\sin 30^{\circ } = 4\cdot \frac{1}{2} = 2,\\[5pt] y &= 4\cos 30^{\circ } = 4\cdot \frac{\sqrt{3}}{2} = 2\sqrt{3}\,\textrm{.} \end{align} |
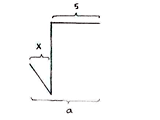
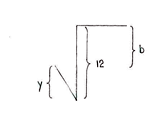
Mit x und y erhalten wir die Katheten a und b, indem wir die horizontalen und vertikalen Abstände in der Figur betrachten.
| 
| |
| \displaystyle \begin{align}a &= x+5\\ &= 2+5 = 7\end{align} | \displaystyle \begin{align}b &= 12-y\\ &= 12-2\sqrt{3}\end{align} |
Mit a und b erhalten wir c durch den Satz des Pythagoras
| \displaystyle \begin{align}
c &= \sqrt{a^2+b^2}\\[5pt] &= \sqrt{7^2+(12-2\sqrt{3})^2}\\[5pt] &= \sqrt{49+(12^2-2\cdot 12\cdot 2\sqrt{3}+(2\sqrt{3})^2)}\\[5pt] &= \sqrt{205-38\sqrt{3}}\\[5pt] &\approx 11\textrm{.}0\ \text{km}\textrm{.} \end{align} |