Lösung 4.1:7a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
| - | In dieser Form ist es schwierig den Mittelpunkt und Radius des Kreises abzulesen. Daher benuzen wir quadratische Ergänzung um die Gleichung auf die Standardform | + | In dieser Form, ist es schwierig den Mittelpunkt und Radius des Kreises abzulesen. Daher benuzen wir quadratische Ergänzung, um die Gleichung auf die Standardform |
{{Abgesetzte Formel||<math>(x-a)^2 + (y-b)^2 = r^2\,,</math>}} | {{Abgesetzte Formel||<math>(x-a)^2 + (y-b)^2 = r^2\,,</math>}} | ||
Version vom 13:52, 16. Jun. 2009
In dieser Form, ist es schwierig den Mittelpunkt und Radius des Kreises abzulesen. Daher benuzen wir quadratische Ergänzung, um die Gleichung auf die Standardform
| \displaystyle (x-a)^2 + (y-b)^2 = r^2\,, |
zu bringen, wo wir den Mittelpunkt und Radius ablesen können.
Wir verwenden uns von quadratischer Ergänzung für jeweils die x- und y-Terme, und erhalten
| \displaystyle \begin{align}
x^2 + 2x &= (x+1)^2-1^2\,,\\[5pt] y^2 - 2y &= (y-1)^2-1^2\,, \end{align} |
Also ist die Gleichung
| \displaystyle (x+1)^2 - 1^2 + (y-1)^2 - 1^2 = 1\,, |
oder auch
| \displaystyle (x+1)^2 + (y-1)^2 = 3\,\textrm{.} |
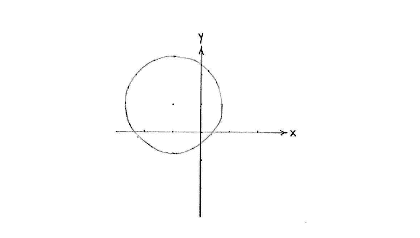
Dies ist die Gleichung eines Kreises mit dem Mittelpunkt (-1,1) und dem Radius \displaystyle \sqrt{3}\,.