Lösung 4.1:4a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
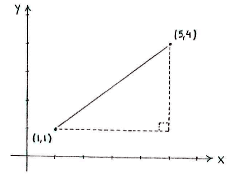
| - | Wir zeichnen die Punkte | + | Wir zeichnen die Punkte und sehen, dass der Abstand zwischen den Punkten die Hypotenuse des Dreiecks ist, wobei die Katheten parallel zu den Koordinatenachsen sind. |
[[Image:4_1_4_a-1(2)_1.gif|center]] | [[Image:4_1_4_a-1(2)_1.gif|center]] | ||
| Zeile 20: | Zeile 20: | ||
| - | Hinweis: Allgemein ist der Abstand d | + | Hinweis: Allgemein ist der Abstand d zwischen den Punkten <math>(x,y)</math> und <math>(a,b)</math> |
{{Abgesetzte Formel||<math>d = \sqrt{(x-a)^2 + (y-b)^2}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>d = \sqrt{(x-a)^2 + (y-b)^2}\,\textrm{.}</math>}} | ||
Version vom 13:42, 16. Jun. 2009
Wir zeichnen die Punkte und sehen, dass der Abstand zwischen den Punkten die Hypotenuse des Dreiecks ist, wobei die Katheten parallel zu den Koordinatenachsen sind.
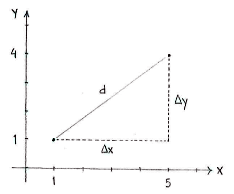
Die Länge der Katheten erhalten wir einfach als den Unterschied des x- und y-Wertes von den beiden Punkten.
| ∆x = 5 - 1 = 4 and ∆y = 4 - 1 = 3 |
Mit dem Gesetz des Pythagoras erhalten wir die Hypotenuse, und so auch den Abstand zwischen den Punkten,
| \displaystyle \begin{align}
d &= \sqrt{(\Delta x)^2 + (\Delta y)^2} = \sqrt{4^2+3^2}\\[5pt] &= \sqrt{16+9} = \sqrt{25} = 5\,\textrm{.} \end{align} |
Hinweis: Allgemein ist der Abstand d zwischen den Punkten \displaystyle (x,y) und \displaystyle (a,b)
| \displaystyle d = \sqrt{(x-a)^2 + (y-b)^2}\,\textrm{.} |