Lösung 2.3:10a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
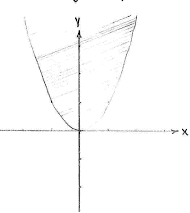
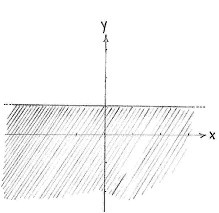
Je für sich, definieren die Ungleichungen <math>y\ge x^{2}</math> und <math>y\le 1</math> das Gebiet oberhalb der Parabel <math>y=x^{2}</math> und das Gebiet unterhalb der Gerade <math>y=1</math>, respectively.
+
Jeweils für sich definieren die Ungleichungen <math>y\ge x^{2}</math> und <math>y\le 1</math> das Gebiet oberhalb der Parabel <math>y=x^{2}</math> und das Gebiet unterhalb der Gerade <math>y=1</math>, respectively.
{| align="center"
{| align="center"
Zeile 6: Zeile 6:
|align="center"|[[Image:2_3_10_a-2.gif|center]]
|align="center"|[[Image:2_3_10_a-2.gif|center]]
|-
|-
-
|align="center"|<small>The region ''y''&nbsp;≥&nbsp;''x''²</small>
+
|align="center"|<small>Das Gebiet ''y''&nbsp;≥&nbsp;''x''²</small>
||
||
-
|align="center"|<small>The region ''y''&nbsp;≤&nbsp;1</small>
+
|align="center"|<small>Das Gebiet ''y''&nbsp;≤&nbsp;1</small>
|}
|}

Version vom 14:04, 9. Jun. 2009

Jeweils für sich definieren die Ungleichungen \displaystyle y\ge x^{2} und \displaystyle y\le 1 das Gebiet oberhalb der Parabel \displaystyle y=x^{2} und das Gebiet unterhalb der Gerade \displaystyle y=1, respectively.

 
Das Gebiet y ≥ x² Das Gebiet y ≤ 1

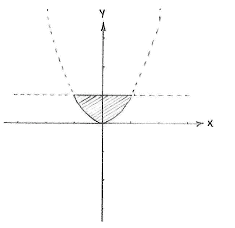
Die Punkte die beide Ungleichungen erfüllen, liegen also zwischen der Geraden und der Parabel.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.3:10a“