Lösung 2.3:6a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
| - | Mit der binomischen Formel <math>(a+b)^2=a^2+2ab+b^2</math> | + | Mit der binomischen Formel <math>(a+b)^2=a^2+2ab+b^2</math> sehen wir, dass der quadratische Ausdruck <math>(x-1)^{2}\,</math> ist |
{{Abgesetzte Formel||<math>x^{2}-2x+1 = (x-1)^{2}\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>x^{2}-2x+1 = (x-1)^{2}\,\textrm{.}</math>}} | ||
| Zeile 7: | Zeile 7: | ||
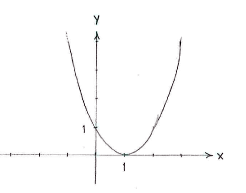
| - | Hinweis: Zeichnen wir die | + | Hinweis: Zeichnen wir die Graph von <math>y=(x-1)^{2}</math>, sehen wir dass die Funktion ein Minimum in <math>x=1\,</math> hat. |
[[Image:2_3_6_a.gif|center]] | [[Image:2_3_6_a.gif|center]] | ||
Version vom 13:55, 9. Jun. 2009
Mit der binomischen Formel \displaystyle (a+b)^2=a^2+2ab+b^2 sehen wir, dass der quadratische Ausdruck \displaystyle (x-1)^{2}\, ist
| \displaystyle x^{2}-2x+1 = (x-1)^{2}\,\textrm{.} |
Die Funktion nimmt ihren kleinsten Wert, null an, wenn \displaystyle x-1=0, also wenn \displaystyle x=1. Alle anderen Werten von \displaystyle x-1 ergeben einen positiven Ausdruck \displaystyle (x-1)^{2}.
Hinweis: Zeichnen wir die Graph von \displaystyle y=(x-1)^{2}, sehen wir dass die Funktion ein Minimum in \displaystyle x=1\, hat.