Lösung 2.2:8b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
(Sprache und Formulierung) |
|||
| Zeile 1: | Zeile 1: | ||
| - | Die Punkte die die Ungleichung <math>y < 3x-4</math> erfüllen, haben eine ''y''-Koordinate die kleiner | + | Die Punkte, die die Ungleichung <math>y < 3x-4</math> erfüllen, haben eine ''y''-Koordinate, die bei gleicher ''x''-Koordinate kleiner ist als die der Geraden <math>y=3x-4</math>. Also besteht das Gebiet aus allen Punkten unterhalb der Gerade <math>y=3x-4</math>. |
[[Image:2_2_8_b.gif|center]] | [[Image:2_2_8_b.gif|center]] | ||
| - | Man kann die Gerade <math>y=3x-4</math> zeichnen, indem man zwei ''x''-Werte wählt, zum Beispiel <math>x=0</math> und <math>x=1</math>, und danach die ''y''-Werte berechnet durch die Gleichung der Gerade. Die ''y''-Werte sind also <math>y=3\cdot 0-4=-4</math> und <math>y=3\cdot 1-4=-1</math>. Wir ziehen jetzt einfach eine Gerade | + | Man kann die Gerade <math>y=3x-4</math> zeichnen, indem man zwei ''x''-Werte wählt, zum Beispiel <math>x=0</math> und <math>x=1</math>, und danach die ''y''-Werte berechnet durch die Gleichung der Gerade. Die ''y''-Werte sind also <math>y=3\cdot 0-4=-4</math> und <math>y=3\cdot 1-4=-1</math>. Wir ziehen jetzt einfach eine Gerade durch die beiden Punkte. |
Version vom 09:56, 9. Jun. 2009
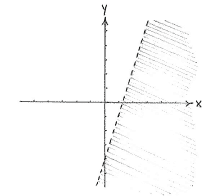
Die Punkte, die die Ungleichung \displaystyle y < 3x-4 erfüllen, haben eine y-Koordinate, die bei gleicher x-Koordinate kleiner ist als die der Geraden \displaystyle y=3x-4. Also besteht das Gebiet aus allen Punkten unterhalb der Gerade \displaystyle y=3x-4.
Man kann die Gerade \displaystyle y=3x-4 zeichnen, indem man zwei x-Werte wählt, zum Beispiel \displaystyle x=0 und \displaystyle x=1, und danach die y-Werte berechnet durch die Gleichung der Gerade. Die y-Werte sind also \displaystyle y=3\cdot 0-4=-4 und \displaystyle y=3\cdot 1-4=-1. Wir ziehen jetzt einfach eine Gerade durch die beiden Punkte.