Lösung 4.2:3c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 4.2:3c“ nach „Lösung 4.2:3c“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
We can add and subtract multiples of <math>2\pi</math> to or from the argument of the sine function without changing its value. The angle <math>2\pi</math> corresponds to a whole turn in a unit circle and the sine function returns to the same value every time the angle changes by a complete revolution.
+
Wir können <math>2\pi</math> vom Winkel addieren oder subtrahieren, ohne dass sich der Wert des Sinus ändert, nachdem <math>2\pi</math> eine ganze umdrehung entspricht.
-
For example, if we can subtract sufficiently many <math>2\pi</math>'s from <math>9\pi</math>, we will obtain a more manageable argument which lies between <math>0</math> and <math>2\pi\,</math>,
+
Zum Beispiel können wir <math>2\pi</math> so oft von <math>9\pi</math> subtrahieren, bis wir einen Winkel zwischen <math>0</math> und <math>2\pi\,</math> erhalten.
{{Abgesetzte Formel||<math>\sin 9\pi = \sin (9\pi - 2\pi - 2\pi - 2\pi - 2\pi) = \sin \pi\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\sin 9\pi = \sin (9\pi - 2\pi - 2\pi - 2\pi - 2\pi) = \sin \pi\,\textrm{.}</math>}}
-
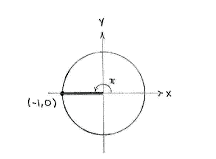
The line which makes an angle <math>\pi</math> with the positive part of the ''x''-axis is the negative part of the ''x''-axis and it cuts the unit circle at the point (-1,0), which is why we can see from the ''y''-coordinate that <math>\sin 9\pi = \sin \pi = 0\,</math>.
+
Die Gerade mit dem Winkel <math>\pi</math> zur positiven ''x''-Achse, ist die negative ''x''-Achse. Die Schnittstelle zwischen dieser Gerade und des Einheitskreises ist der Punkt (-1,0), und die ''y''-Koordinate von diesen Punkt ist gleich <math>\sin 9\pi = \sin \pi = 0\,</math>.
[[Image:4_2_3_c.gif|center]]
[[Image:4_2_3_c.gif|center]]

Version vom 12:29, 4. Apr. 2009

Wir können \displaystyle 2\pi vom Winkel addieren oder subtrahieren, ohne dass sich der Wert des Sinus ändert, nachdem \displaystyle 2\pi eine ganze umdrehung entspricht.

Zum Beispiel können wir \displaystyle 2\pi so oft von \displaystyle 9\pi subtrahieren, bis wir einen Winkel zwischen \displaystyle 0 und \displaystyle 2\pi\, erhalten.

\displaystyle \sin 9\pi = \sin (9\pi - 2\pi - 2\pi - 2\pi - 2\pi) = \sin \pi\,\textrm{.}

Die Gerade mit dem Winkel \displaystyle \pi zur positiven x-Achse, ist die negative x-Achse. Die Schnittstelle zwischen dieser Gerade und des Einheitskreises ist der Punkt (-1,0), und die y-Koordinate von diesen Punkt ist gleich \displaystyle \sin 9\pi = \sin \pi = 0\,.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:3c“