Lösung 2.3:8c
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K (hat „Solution 2.3:8c“ nach „Lösung 2.3:8c“ verschoben: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | Durch quadratische Ergänzung können wir den Ausdruck umschreiben | |
{{Abgesetzte Formel||<math>f(x) = x^{2}-6x+11 = (x-3)^{2} - 3^{2} + 11 = (x-3)^{2} + 2,</math>}} | {{Abgesetzte Formel||<math>f(x) = x^{2}-6x+11 = (x-3)^{2} - 3^{2} + 11 = (x-3)^{2} + 2,</math>}} | ||
| - | + | So sehen wir dass der Graph von der Funktion <math>y = (x-3)^{2} + 2</math> der Graph von der Funktion <math>y=x^{2}</math> ist, nur zwei Einheiten nach oben, und drei Einheiten nach rechts verschoben (Sehen Sie 8a und 8b). | |
Version vom 19:29, 16. Mär. 2009
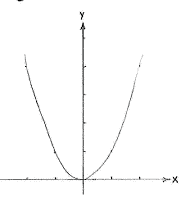
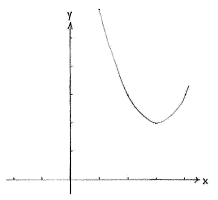
Durch quadratische Ergänzung können wir den Ausdruck umschreiben
| \displaystyle f(x) = x^{2}-6x+11 = (x-3)^{2} - 3^{2} + 11 = (x-3)^{2} + 2, |
So sehen wir dass der Graph von der Funktion \displaystyle y = (x-3)^{2} + 2 der Graph von der Funktion \displaystyle y=x^{2} ist, nur zwei Einheiten nach oben, und drei Einheiten nach rechts verschoben (Sehen Sie 8a und 8b).
| The graph of f(x) = x² | The graph of f(x) = x² - 6x + 11 |