Lösung 2.2:9c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 2.2:9c“ nach „Lösung 2.2:9c“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
First, we draw the regions which the various inequalities define.
+
Wir zeichnen zuerst die Gebiete die durch die drei Ungleichungen entstehen.
{| align="center"
{| align="center"
Zeile 13: Zeile 13:
|}
|}
-
The triangle is defined as those points which satisfy all inequalities, which is the region which the three grey areas have in common.
+
Das Dreieck ist das Gebiet dass wo die Punkte alle dre Ungleichungen erfüllen, also das Gebiet das alle grau gefärbten Gebiete enthält.
Zeile 19: Zeile 19:
-
Before we start thinking about how we should calculate the area of the triangle, we must determine the corner points of the triangle.
+
Als erster Schritt müssen wir die Schnittpunkte der Geraden berechnen, die also auch die Ecken des Dreiecks sind.
-
If we write equations for the edges in pairs
+
Die drei Ecken müssen jeweils die Drei Gleichungssysteme unten erfüllen
{{Abgesetzte Formel||<math>(1)\ \left\{\begin{align} x+y&=-2,\\ 2x-y&=2,\end{align}\right.\qquad
{{Abgesetzte Formel||<math>(1)\ \left\{\begin{align} x+y&=-2,\\ 2x-y&=2,\end{align}\right.\qquad
Zeile 28: Zeile 28:
(3)\ \left\{\begin{align} 2x-y &= 2,\\ -x+2y &= 2,\end{align}\right.</math>}}
(3)\ \left\{\begin{align} 2x-y &= 2,\\ -x+2y &= 2,\end{align}\right.</math>}}
-
we obtain an equation system which determines the points of intersections between respective pairs of lines, and these points correspond to the triangle's corners.
 
<ol>
<ol>
-
<li>We can solve the first system by summing the two equations:
+
<li>Das erste Gleichungssystem lösen wir indem wir die beiden Gleichungen addieren
{| align="center" style="padding:10px 0px 10px 0px;"
{| align="center" style="padding:10px 0px 10px 0px;"
||
||
Zeile 57: Zeile 56:
|}
|}
-
Thus, we obtain <math>x=0</math> and, from the equation <math>x+y=-2</math>, that <math>y=-2</math>.</li>
+
So erhalten wir also <math>x=0</math>, und von der Glcihung <math>x+y=-2</math> erhalten wir <math>y=-2</math>.</li>
-
<li>In the same way, we sum the equations in the second system,
+
<li>Im zweiten System können wir die Gleichungen genauso addieren
{| align="center" style="padding:10px 0px 10px 0px;"
{| align="center" style="padding:10px 0px 10px 0px;"
||
||
Zeile 84: Zeile 83:
|}
|}
-
which gives <math>y=0</math> and <math>x=-2</math>.</li>
+
Wir erhalten also <math>y=0</math> und <math>x=-2</math>.</li>
-
<li>The final equation system is a little trickier to solve, but if we make ''y'' the subject in the first equation, so that <math>y=2x-2</math>, and substitute it into the second equation, we get
+
 
 +
<li>Das dritte System ist ein wenig schwieriger zu lösen. Hier müssen wir ''y'' in der zweiten Gleichung mit <math>2x-2</math> ersetzen (von der ersten Gleichung), und danach ''x'' in die erste Gleichung einsetzen.
{{Abgesetzte Formel||<math>-x+(2x-2)=2\quad\Leftrightarrow\quad 3x-4=2\quad\Leftrightarrow\quad x=2\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>-x+(2x-2)=2\quad\Leftrightarrow\quad 3x-4=2\quad\Leftrightarrow\quad x=2\,\textrm{.}</math>}}
-
The corresponding value for ''y'' is <math>y=2\cdot 2-2 = 2\,\textrm{.}</math></li>
+
Und also ist <math>y=2\cdot 2-2 = 2\,\textrm{.}</math></li>
</ol>
</ol>
-
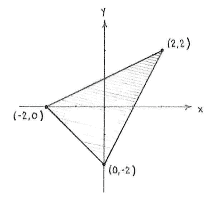
The triangle's corner points are thus (0,-2), (-2,0) and (2,2).
+
Die Ecken des Dreiecks sind also (0,-2), (-2,0) und (2,2).
Zeile 98: Zeile 98:
-
The problem we have in calculating the area of the triangle with the formula
+
Wenn wir die Fläche des Dreiecks mit der Gleichung
{{Abgesetzte Formel||<math>\text{Area} = \tfrac{1}{2}\text{(base)}\cdot\text{(height)}</math>}}
{{Abgesetzte Formel||<math>\text{Area} = \tfrac{1}{2}\text{(base)}\cdot\text{(height)}</math>}}
-
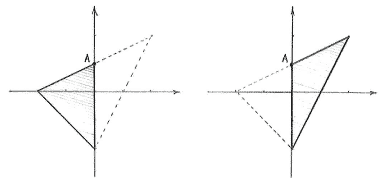
is that there is no natural base for the triangle, since none of the edges are parallel with any of the coordinate axes. On the other hand, what we can do is to divide up the triangle along the ''y''-axis and obtain two sub-triangles where we use the ''y''-axis as the base.
+
berechnen, ist das Problem die Basis und die Höhe des Dreiecks zu berechnen, nachdem keine Kante mit der ''x''- oder ''y''-Achse parallel ist. Wir können aber das Dreieck in zwei Dreiecke aufteilen, die beide eine Kante haben, die parallel mit der ''y''-Achse ist.
[[Image:2_2_9_c-4(5).gif|center]]
[[Image:2_2_9_c-4(5).gif|center]]
-
 
+
Hier entsteht ein neuer Eckpunkt, A, den wir berechnen müssen. Wir sehen dass der Punkt A die Schnittstelle zwischen der Gerade <math>2y-x=\text{2 }</math> und der ''y''-Achse ist
-
This division creates a new corner point for the triangles (marked A in the figure above) and we can determine it to be the intersection point between the line
+
-
<math>2y-x=\text{2 }</math> and the ''y''-axis
+
{{Abgesetzte Formel||<math>\left\{\begin{align} 2y-x&=2\\ x&=0\\ \end{align}\right.</math>}}
{{Abgesetzte Formel||<math>\left\{\begin{align} 2y-x&=2\\ x&=0\\ \end{align}\right.</math>}}
-
which gives that the new corner point is at (0,1).
+
Die Schnittstelle, und der Punkt A, ist also (0,1).
-
We now have all the information we need for calculating the base, height and area of the two sub-triangles.
+
Jetzt können wir einfach die Flächen des beiden Dreiecken berechnen

Version vom 13:54, 13. Mär. 2009

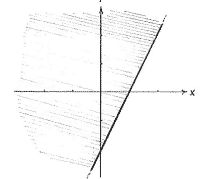
Wir zeichnen zuerst die Gebiete die durch die drei Ungleichungen entstehen.

The region x + y ≥ -2 The region 2x - y ≤ 2
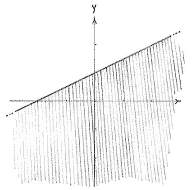
The region 2y - x ≤ 2

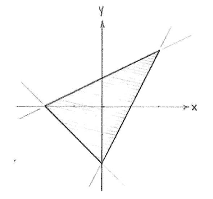
Das Dreieck ist das Gebiet dass wo die Punkte alle dre Ungleichungen erfüllen, also das Gebiet das alle grau gefärbten Gebiete enthält.



Als erster Schritt müssen wir die Schnittpunkte der Geraden berechnen, die also auch die Ecken des Dreiecks sind.

Die drei Ecken müssen jeweils die Drei Gleichungssysteme unten erfüllen

\displaystyle (1)\ \left\{\begin{align} x+y&=-2,\\ 2x-y&=2,\end{align}\right.\qquad

(2)\ \left\{\begin{align} x+y &= -2,\\ -x+2y &= 2,\end{align}\right.\qquad \text{and}\qquad (3)\ \left\{\begin{align} 2x-y &= 2,\\ -x+2y &= 2,\end{align}\right.


  1. Das erste Gleichungssystem lösen wir indem wir die beiden Gleichungen addieren
    \displaystyle x \displaystyle {}+{} \displaystyle y \displaystyle {}={} \displaystyle -2
    \displaystyle +\ \ \displaystyle 2x \displaystyle {}-{} \displaystyle y \displaystyle {}={} \displaystyle 2
    \displaystyle 3x \displaystyle {}={} \displaystyle 0
    So erhalten wir also \displaystyle x=0, und von der Glcihung \displaystyle x+y=-2 erhalten wir \displaystyle y=-2.
  2. Im zweiten System können wir die Gleichungen genauso addieren
    \displaystyle x \displaystyle {}+{} \displaystyle y \displaystyle {}={} \displaystyle -2
    \displaystyle +\ \ \displaystyle -x \displaystyle {}+{} \displaystyle 2y \displaystyle {}={} \displaystyle 2
    \displaystyle 3x \displaystyle {}={} \displaystyle 0
    Wir erhalten also \displaystyle y=0 und \displaystyle x=-2.
  3. Das dritte System ist ein wenig schwieriger zu lösen. Hier müssen wir y in der zweiten Gleichung mit \displaystyle 2x-2 ersetzen (von der ersten Gleichung), und danach x in die erste Gleichung einsetzen.
    \displaystyle -x+(2x-2)=2\quad\Leftrightarrow\quad 3x-4=2\quad\Leftrightarrow\quad x=2\,\textrm{.}
    Und also ist \displaystyle y=2\cdot 2-2 = 2\,\textrm{.}

Die Ecken des Dreiecks sind also (0,-2), (-2,0) und (2,2).



Wenn wir die Fläche des Dreiecks mit der Gleichung

\displaystyle \text{Area} = \tfrac{1}{2}\text{(base)}\cdot\text{(height)}

berechnen, ist das Problem die Basis und die Höhe des Dreiecks zu berechnen, nachdem keine Kante mit der x- oder y-Achse parallel ist. Wir können aber das Dreieck in zwei Dreiecke aufteilen, die beide eine Kante haben, die parallel mit der y-Achse ist.


Hier entsteht ein neuer Eckpunkt, A, den wir berechnen müssen. Wir sehen dass der Punkt A die Schnittstelle zwischen der Gerade \displaystyle 2y-x=\text{2 } und der y-Achse ist

\displaystyle \left\{\begin{align} 2y-x&=2\\ x&=0\\ \end{align}\right.

Die Schnittstelle, und der Punkt A, ist also (0,1).

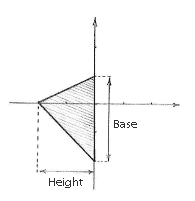
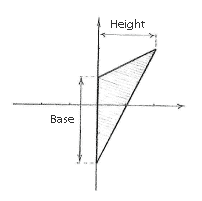
Jetzt können wir einfach die Flächen des beiden Dreiecken berechnen


Image:2_2_9_c-5(5)-1.gif Image:2_2_9_c-5(5)-2.gif
base  =  1 - (-2) = 3   base  =  1 - (-2) = 3
height  =  0 - (-2) = 2   height  =  2 - 0 = 2
area  =  ½·3·2 = 3 area  =  ½·3·2 = 3


Finally, it remains only to add up the sub-areas to get the total area of the triangle:

\displaystyle \text{Area} = 3+3=6\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:9c“