Lösung 2.2:9a

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (hat „Solution 2.2:9a“ nach „Lösung 2.2:9a“ verschoben: Robot: moved page)
Zeile 1: Zeile 1:
-
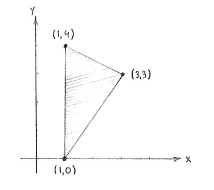
We can start by drawing the points (1,4), (3,3) and (1,0) in a coordinate system and draw lines between them, so that we get a picture of how the triangle looks like.
+
Wir beginne damit, die Punkte (1,4), (3,3) and (1,0), sodass wir sehen wie das Dreieck aussieht.
-
 
+
[[Image:2_2_9_a-1(2).gif|center]]
[[Image:2_2_9_a-1(2).gif|center]]
 +
Die Fläche eines Dreiecks ist
-
If we now think of how we should use the fact that the area of a triangle is given by the formula
+
{{Abgesetzte Formel||<math>\text{Fläche} = \frac{1}{2}\cdot\text{(Basis)}\cdot\text{(Höhe),}</math>}}
-
 
+
-
{{Abgesetzte Formel||<math>\text{Area} = \frac{1}{2}\cdot\text{(base)}\cdot\text{(height),}</math>}}
+
-
it is clear that it is most appropriate to use the edge from (1,0) to (1,4) as the base of the triangle. The base is then parallel with the ''y''-axis and we can read off its length as the difference in the ''y''-coordinate between the corner points (1,0) and (1,4), i.e.
+
Nachdem die Kante zwischen den Punkten (1,0) und (1,4) parallel mit der ''y''-Achse ist, bezeichnen wir diese Kante als Basis. Die Basis des Dreiecks ist der Unterschied zwischen den ''y''-Koordinaten von den Punkten (1,0) und (1,4)
{{Abgesetzte Formel||<math>\text{base} = 4-0 = 4\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\text{base} = 4-0 = 4\,\textrm{.}</math>}}
-
In addition, the triangle's height is the horizontal distance from the third corner point (3,3) to the base and we can read that off as the difference in the ''x''-direction between (3,3) and the line <math>x=1</math>, i.e.
+
Die Höhe des Dreiecks ist der Unterschied zwischen den ''x''-Koordinaten zwischen den Punkt (3,3), und der Gerade <math>x=1</math>
{{Abgesetzte Formel||<math>\text{height} = 3-1 = 2\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\text{height} = 3-1 = 2\,\textrm{.}</math>}}
Zeile 21: Zeile 19:
-
Thus, the triangle's area is
+
Also ist die Fläche des Dreiecks
{{Abgesetzte Formel||<math>\text{Area} = \tfrac{1}{2}\cdot\textrm{(base)}\cdot\textrm{(height)} = \tfrac{1}{2}\cdot 4\cdot 2 = 4\,\text{u.a.}</math>}}
{{Abgesetzte Formel||<math>\text{Area} = \tfrac{1}{2}\cdot\textrm{(base)}\cdot\textrm{(height)} = \tfrac{1}{2}\cdot 4\cdot 2 = 4\,\text{u.a.}</math>}}

Version vom 12:59, 13. Mär. 2009

Wir beginne damit, die Punkte (1,4), (3,3) and (1,0), sodass wir sehen wie das Dreieck aussieht.

Die Fläche eines Dreiecks ist

\displaystyle \text{Fläche} = \frac{1}{2}\cdot\text{(Basis)}\cdot\text{(Höhe),}

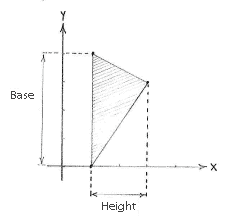
Nachdem die Kante zwischen den Punkten (1,0) und (1,4) parallel mit der y-Achse ist, bezeichnen wir diese Kante als Basis. Die Basis des Dreiecks ist der Unterschied zwischen den y-Koordinaten von den Punkten (1,0) und (1,4)

\displaystyle \text{base} = 4-0 = 4\,\textrm{.}

Die Höhe des Dreiecks ist der Unterschied zwischen den x-Koordinaten zwischen den Punkt (3,3), und der Gerade \displaystyle x=1

\displaystyle \text{height} = 3-1 = 2\,\textrm{.}



Also ist die Fläche des Dreiecks

\displaystyle \text{Area} = \tfrac{1}{2}\cdot\textrm{(base)}\cdot\textrm{(height)} = \tfrac{1}{2}\cdot 4\cdot 2 = 4\,\text{u.a.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:9a“