Lösung 4.1:10
Aus Online Mathematik Brückenkurs 1
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
K (hat „Solution 4.1:10“ nach „Lösung 4.1:10“ verschoben: Robot: moved page) |
Version vom 14:43, 22. Okt. 2008
First, let's decide to determine all distance in dm (decimeters), so that we have all the distances as integers.
Call the length of the washing line from the trees to the hanger y and z, as in the figure below, and introduce two auxiliary triangles which have y and z as their hypotenuses. (As an approximation, we suppose that the taut washing line consists of two straight parts.)
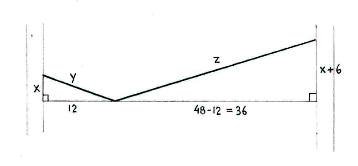
Because the line is 54 dm long, we have
| \displaystyle y+z=54\,\textrm{.} | (1) |
Then, the Pythagorean theorem gives the relations
| \displaystyle y^2 = x^2 + 12^2\,, | (2) |
| \displaystyle z^2 = (x+6)^2 + 36^2\,\textrm{.} | (3) |
The idea now is to solve the system of equations (1)-(3) by first eliminating z, so that we get two equations which only contain x and y. Then, eliminate y from one of these equations, so that we get an equation which determines x.
From (1), we have \displaystyle z = 54-y, and substituting this into (3) gives us the equation
| \displaystyle (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.} | (3') |
Equations (2) and (3') together give a smaller system for x and y,
| \displaystyle \left\{ \begin{align}
& y^2 = x^2 + 12^2\,,\\[5pt] & (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.} \end{align} \right. | \displaystyle \begin{align}(2)\\[5pt] (3')\end{align} |
Expand the quadratic terms on both sides of (3'),
| \displaystyle 54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,, |
and simplify
| \displaystyle 2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.} |
Use (2) and replace \displaystyle y^2 with \displaystyle x^2+12 in this equation,
| \displaystyle 2916 - 108y + x^2 + 144 = x^2 + 12x + 1332 |
which gets rid of the x²-term,
| \displaystyle 2916 - 108y + 144 = 12x + 1332\,, |
and further simplification gives the equation
| \displaystyle 12x + 108y = 1728 | (3") |
If we pause for a moment and summarize the situation, we see that we have succeeded in simplifying the equation system (2) and (3') to a system (2) and (3"), where one of the equations is linear
| \displaystyle \left\{ \begin{align}
& y^2 = x^2 + 12^2\,,\\[5pt] & 12x+108y=1728\,\textrm{.} \end{align} \right. | \displaystyle \begin{align}(2)\\[5pt] (3")\end{align} |
In this system, we can make y the subject in (3"),
| \displaystyle y=\frac{1728-12x}{108}=16-\frac{x}{9} |
and substitute into (2),
| \displaystyle \Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.} |
This is an equation which only contains x, and if we solve it, we will get our answer.
Expand the quadratic on the left-hand side,
| \displaystyle 16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144 |
and collect together all terms on one side,
| \displaystyle x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,, |
which gives the equation
| \displaystyle \frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.} |
Multiply both sides by \displaystyle 81/80 so that we get the equation in standard form,
| \displaystyle x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.} |
Completing the square on the left-hand side gives
| \displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0 |
and then
| \displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,, |
i.e.
| \displaystyle x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.} |
This means that the equation has the solutions
| \displaystyle x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{and}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.} |
The answer is thus \displaystyle x=9\ \textrm{dm} (the negative root must be discarded).
To be sure that we have calculated correctly, we also look at the values of y and z, and check that the original equations (1) to (3) are satisfied.
Equation (3") gives
| \displaystyle y = 16-\frac{x}{9} = 16-1 = 15 |
and equation (1) gives
| \displaystyle z=54-y=54-15=39\,\textrm{.} |
Now, we check that \displaystyle x=9, \displaystyle y=15 and \displaystyle z=39 satisfy the equations (1), (2) and (3),
| \displaystyle \begin{align}
\textrm{LHS of (1)} &= 15+39 = 54\,,\\[5pt] \textrm{RHS of (1)} &= 54\,,\\[10pt] \textrm{LHS of (2)} &= 15^2 = 225\,,\\[5pt] \textrm{RHS of (2)} &= 9^2 + 12^2 = 81+144 = 225\,,\\[10pt] \textrm{LHS of (3)} &= 39^2 = 1521\,,\\[5pt] \textrm{RHS of (3)} &= (9+6)^2 + 36^2 = 15^2 + 36^2 = 225+1296 = 1521\,\textrm{.} \end{align} |
