Lösung 2.2:9a
Aus Online Mathematik Brückenkurs 1
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
K (hat „Solution 2.2:9a“ nach „Lösung 2.2:9a“ verschoben: Robot: moved page) |
Version vom 14:02, 22. Okt. 2008
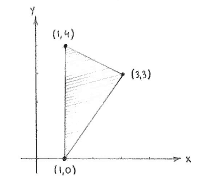
We can start by drawing the points (1,4), (3,3) and (1,0) in a coordinate system and draw lines between them, so that we get a picture of how the triangle looks like.
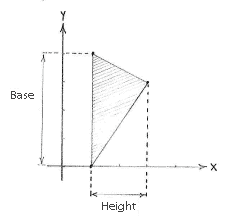
If we now think of how we should use the fact that the area of a triangle is given by the formula
| \displaystyle \text{Area} = \frac{1}{2}\cdot\text{(base)}\cdot\text{(height),} |
it is clear that it is most appropriate to use the edge from (1,0) to (1,4) as the base of the triangle. The base is then parallel with the y-axis and we can read off its length as the difference in the y-coordinate between the corner points (1,0) and (1,4), i.e.
| \displaystyle \text{base} = 4-0 = 4\,\textrm{.} |
In addition, the triangle's height is the horizontal distance from the third corner point (3,3) to the base and we can read that off as the difference in the x-direction between (3,3) and the line \displaystyle x=1, i.e.
| \displaystyle \text{height} = 3-1 = 2\,\textrm{.} |
Thus, the triangle's area is
| \displaystyle \text{Area} = \tfrac{1}{2}\cdot\textrm{(base)}\cdot\textrm{(height)} = \tfrac{1}{2}\cdot 4\cdot 2 = 4\,\text{u.a.} |