Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Lösung 4.4:2c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 5: Zeile 5:
We get the full solution when we add multiples of <math>2\pi</math>,
We get the full solution when we add multiples of <math>2\pi</math>,
-
{{Displayed math||<math>x = 0+2n\pi\qquad\text{and}\qquad x = \pi + 2n\pi\,,</math>}}
+
{{Abgesetzte Formel||<math>x = 0+2n\pi\qquad\text{and}\qquad x = \pi + 2n\pi\,,</math>}}
where ''n'' is an arbitrary integer.
where ''n'' is an arbitrary integer.
Zeile 12: Zeile 12:
Note: Because the difference between <math>0</math> and <math>\pi</math> is a half turn, the solutions are repeated every half turn and they can be summarized in one expression,
Note: Because the difference between <math>0</math> and <math>\pi</math> is a half turn, the solutions are repeated every half turn and they can be summarized in one expression,
-
{{Displayed math||<math>x=0+n\pi\,,</math>}}
+
{{Abgesetzte Formel||<math>x=0+n\pi\,,</math>}}
where ''n'' is an arbitrary integer.
where ''n'' is an arbitrary integer.

Version vom 08:58, 22. Okt. 2008

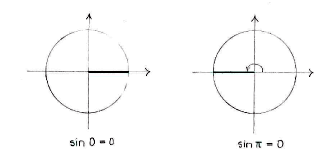
There are two angles in the unit circle, x=0 and x=, whose sine has a value of zero.

We get the full solution when we add multiples of 2,

x=0+2nandx=+2n

where n is an arbitrary integer.


Note: Because the difference between 0 and is a half turn, the solutions are repeated every half turn and they can be summarized in one expression,

x=0+n

where n is an arbitrary integer.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:2c“