Lösung 4.4:1g

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 13: Zeile 13:
The Pythagorean theorem gives
The Pythagorean theorem gives
-
{{Displayed math||<math>x^2 + \Bigl(\frac{x}{\sqrt{3}}\Bigr)^2 = 1^2</math>}}
+
{{Abgesetzte Formel||<math>x^2 + \Bigl(\frac{x}{\sqrt{3}}\Bigr)^2 = 1^2</math>}}
and this equation has the solution <math>x = \sqrt{3}/2</math>, which means that
and this equation has the solution <math>x = \sqrt{3}/2</math>, which means that
-
{{Displayed math||<math>\cos\alpha = \frac{\sqrt{3}/2}{1} = \frac{\sqrt{3}}{2}\,,</math>}}
+
{{Abgesetzte Formel||<math>\cos\alpha = \frac{\sqrt{3}/2}{1} = \frac{\sqrt{3}}{2}\,,</math>}}
i.e. <math>\alpha = \pi/6</math>. Because the angle <math>v</math> in the fourth quadrant is the complement of <math>\alpha</math> the angle <math>v</math> is given by
i.e. <math>\alpha = \pi/6</math>. Because the angle <math>v</math> in the fourth quadrant is the complement of <math>\alpha</math> the angle <math>v</math> is given by
-
{{Displayed math||<math>v = 2\pi - \alpha = 2\pi - \frac{\pi}{6} = \frac{11\pi }{6}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>v = 2\pi - \alpha = 2\pi - \frac{\pi}{6} = \frac{11\pi }{6}\,\textrm{.}</math>}}
If we subtract half a turn, <math>\pi</math>, we obtain the other angle
If we subtract half a turn, <math>\pi</math>, we obtain the other angle
-
{{Displayed math||<math>v = \frac{11\pi}{6} - \pi = \frac{5\pi}{6}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>v = \frac{11\pi}{6} - \pi = \frac{5\pi}{6}\,\textrm{.}</math>}}

Version vom 08:57, 22. Okt. 2008

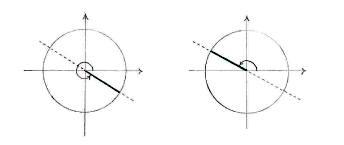
A quick sketch of the unit circle and the line \displaystyle y=(-1/\!\sqrt{3})x, which corresponds to the tangent value \displaystyle -1/\!\sqrt{3} shows that there are two angles which satisfy \displaystyle \tan v = -1/\!\sqrt{3}. One of the angles lies in the fourth quadrant and the other is the opposite angle in the second quadrant.

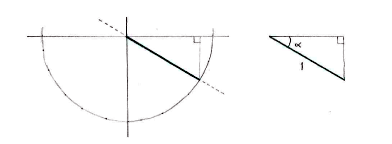
We can therefore limit ourselves to the fourth quadrant and draw an auxiliary triangle in order to determine the angle there.

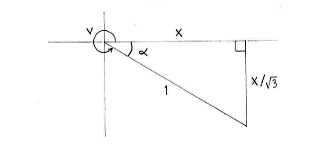
If we call \displaystyle x the side adjacent to the angle \displaystyle \alpha then the fact that \displaystyle \tan v=-1/\!\sqrt{3} gives the length of the opposite side as \displaystyle x/\!\sqrt{3}.

The Pythagorean theorem gives

\displaystyle x^2 + \Bigl(\frac{x}{\sqrt{3}}\Bigr)^2 = 1^2

and this equation has the solution \displaystyle x = \sqrt{3}/2, which means that

\displaystyle \cos\alpha = \frac{\sqrt{3}/2}{1} = \frac{\sqrt{3}}{2}\,,

i.e. \displaystyle \alpha = \pi/6. Because the angle \displaystyle v in the fourth quadrant is the complement of \displaystyle \alpha the angle \displaystyle v is given by

\displaystyle v = 2\pi - \alpha = 2\pi - \frac{\pi}{6} = \frac{11\pi }{6}\,\textrm{.}

If we subtract half a turn, \displaystyle \pi, we obtain the other angle

\displaystyle v = \frac{11\pi}{6} - \pi = \frac{5\pi}{6}\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:1g“