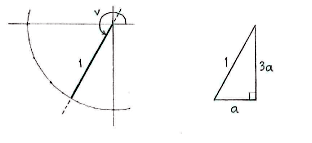Lösung 4.3:6c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 10: Zeile 10:
If we now use the Pythagorean theorem on the triangle, we see that the horizontal side ''a'' satisfies
If we now use the Pythagorean theorem on the triangle, we see that the horizontal side ''a'' satisfies
-
{{Displayed math||<math>a^2 + (3a)^2 = 1^2</math>}}
+
{{Abgesetzte Formel||<math>a^2 + (3a)^2 = 1^2</math>}}
which gives us that <math>10a^{2}=1</math> i.e. <math>a = 1/\!\sqrt{10}\,\textrm{.}</math>
which gives us that <math>10a^{2}=1</math> i.e. <math>a = 1/\!\sqrt{10}\,\textrm{.}</math>
Zeile 16: Zeile 16:
Thus, the angle ''v'''s ''x''-coordinate is <math>-1/\!\sqrt{10}</math> and ''y''-coordinate is <math>-3/\!\sqrt{10}</math>, i.e.
Thus, the angle ''v'''s ''x''-coordinate is <math>-1/\!\sqrt{10}</math> and ''y''-coordinate is <math>-3/\!\sqrt{10}</math>, i.e.
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
\cos v &= -\frac{1}{\sqrt{10}}\,,\\[5pt]
\cos v &= -\frac{1}{\sqrt{10}}\,,\\[5pt]
\sin v &= -\frac{3}{\sqrt{10}}\,\textrm{.}
\sin v &= -\frac{3}{\sqrt{10}}\,\textrm{.}
\end{align}</math>}}
\end{align}</math>}}

Version vom 08:56, 22. Okt. 2008

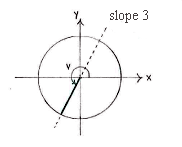
Because the angle \displaystyle v satisfies \displaystyle \pi \le v\le 3\pi/2\,, \displaystyle v belongs to the third quadrant in the unit circle. Furthermore, \displaystyle \tan v = 3 gives that the line which corresponds to the angle \displaystyle v has slope 3.

In the third quadrant, we can introduce a right-angled triangle in which the hypotenuse is 1 and the sides have a 3:1 ratio.

If we now use the Pythagorean theorem on the triangle, we see that the horizontal side a satisfies

\displaystyle a^2 + (3a)^2 = 1^2

which gives us that \displaystyle 10a^{2}=1 i.e. \displaystyle a = 1/\!\sqrt{10}\,\textrm{.}

Thus, the angle v's x-coordinate is \displaystyle -1/\!\sqrt{10} and y-coordinate is \displaystyle -3/\!\sqrt{10}, i.e.

\displaystyle \begin{align}

\cos v &= -\frac{1}{\sqrt{10}}\,,\\[5pt] \sin v &= -\frac{3}{\sqrt{10}}\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.3:6c“