Lösung 4.2:2f
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 5: | Zeile 5: | ||
If we look at one of the triangles, we can set up the trigonometrical relation | If we look at one of the triangles, we can set up the trigonometrical relation | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\sin\frac{v}{2} = \frac{1}{3}\,,</math>}} |
which is an equation for ''v''. | which is an equation for ''v''. | ||
Version vom 08:51, 22. Okt. 2008
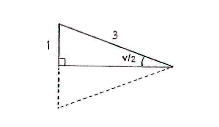
Because the triangle is isosceles (two sides have the same length), it can be divided up into two right-angled triangles of the same size by introducing a side which divides the angle v in half.
If we look at one of the triangles, we can set up the trigonometrical relation
| \displaystyle \sin\frac{v}{2} = \frac{1}{3}\,, |
which is an equation for v.