Aus Online Mathematik Brückenkurs 1

Version vom 14:05, 8. Okt. 2008 (bearbeiten) Tek (Diskussion | Beiträge) K ← Zum vorherigen Versionsunterschied		Version vom 08:50, 22. Okt. 2008 (bearbeiten) (rückgängig) Tekbot (Diskussion | Beiträge) K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) Zum nächsten Versionsunterschied →
Zeile 5:		Zeile 5:
	The opposite is given, whilst it is the adjacent that we are looking for. The tangent of the angle is given by		The opposite is given, whilst it is the adjacent that we are looking for. The tangent of the angle is given by
-	{{Displayed math||<math>\tan 40^{\circ } = \frac{14}{x}</math>}}	+	{{Abgesetzte Formel||<math>\tan 40^{\circ } = \frac{14}{x}</math>}}
	and thus		and thus
-	{{Displayed math||<math>x = \frac{14}{\tan 40^{\circ }}\quad \left( \approx 16\textrm{.}7 \right)\,\textrm{.}</math>}}	+	{{Abgesetzte Formel||<math>x = \frac{14}{\tan 40^{\circ }}\quad \left( \approx 16\textrm{.}7 \right)\,\textrm{.}</math>}}

---

Version vom 08:50, 22. Okt. 2008

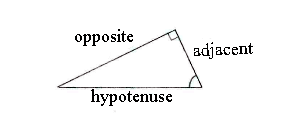
The difficulty is to recognize the sides in the right-angled triangle. A simple rule of thumb is that the hypotenuse is the side which is opposite the right angle (it is also the longest side in the triangle). The adjacent is the side which lies near to the angle that we are considering and the opposite is the third side.

The opposite is given, whilst it is the adjacent that we are looking for. The tangent of the angle is given by

\displaystyle \tan 40^{\circ } = \frac{14}{x}

and thus

\displaystyle x = \frac{14}{\tan 40^{\circ }}\quad \left( \approx 16\textrm{.}7 \right)\,\textrm{.}