Lösung 4.1:6b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 1: Zeile 1:
A quick way to interpret the equation is to compare it with the standard formula for the equation of a circle with centre at (''a'',''b'') and radius ''r'',
A quick way to interpret the equation is to compare it with the standard formula for the equation of a circle with centre at (''a'',''b'') and radius ''r'',
-
{{Displayed math||<math>(x-a)^2 + (y-b)^2 = r^2\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>(x-a)^2 + (y-b)^2 = r^2\,\textrm{.}</math>}}
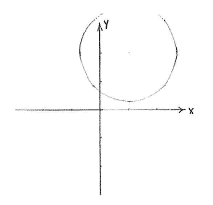
In our case, we can write the equation as
In our case, we can write the equation as
-
{{Displayed math||<math>(x-1)^2 + (y-2)^2 = (\sqrt{3})^2</math>}}
+
{{Abgesetzte Formel||<math>(x-1)^2 + (y-2)^2 = (\sqrt{3})^2</math>}}
and then we see that it describes a circle with centre at (1,2) and radius <math>\sqrt{3}\,</math>.
and then we see that it describes a circle with centre at (1,2) and radius <math>\sqrt{3}\,</math>.

Version vom 08:48, 22. Okt. 2008

A quick way to interpret the equation is to compare it with the standard formula for the equation of a circle with centre at (a,b) and radius r,

\displaystyle (x-a)^2 + (y-b)^2 = r^2\,\textrm{.}

In our case, we can write the equation as

\displaystyle (x-1)^2 + (y-2)^2 = (\sqrt{3})^2

and then we see that it describes a circle with centre at (1,2) and radius \displaystyle \sqrt{3}\,.


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.1:6b“