Lösung 4.1:5b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 1: Zeile 1:
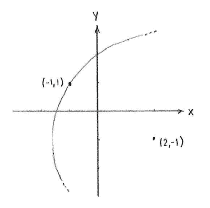
If the circle is to contain the point (-1,1), then that point's distance away from the centre (2,-1) must equal the circle's radius, ''r''. Thus, we can obtain the circle's radius by calculating the distance between (-1,1) and (2,-1) using the distance formula,
If the circle is to contain the point (-1,1), then that point's distance away from the centre (2,-1) must equal the circle's radius, ''r''. Thus, we can obtain the circle's radius by calculating the distance between (-1,1) and (2,-1) using the distance formula,
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
r &= \sqrt{(2-(-1))^2+(-1-1)^2} = \sqrt{3^2+(-2)^2} = \sqrt{9+4} = \sqrt{13}\,\textrm{.}
r &= \sqrt{(2-(-1))^2+(-1-1)^2} = \sqrt{3^2+(-2)^2} = \sqrt{9+4} = \sqrt{13}\,\textrm{.}
\end{align}</math>}}
\end{align}</math>}}
Zeile 7: Zeile 7:
When we know the circle's centre and its radius, we can write the equation of the circle,
When we know the circle's centre and its radius, we can write the equation of the circle,
-
{{Displayed math||<math>(x-2)^2 + (y-(-1))^2 = (\sqrt{13})^{2}</math>}}
+
{{Abgesetzte Formel||<math>(x-2)^2 + (y-(-1))^2 = (\sqrt{13})^{2}</math>}}
which the same as
which the same as
-
{{Displayed math||<math>(x-2)^{2} + (y+1)^2 = 13\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>(x-2)^{2} + (y+1)^2 = 13\,\textrm{.}</math>}}
Zeile 19: Zeile 19:
Note: A circle having its centre at (''a'',''b'') and radius ''r'' has the equation
Note: A circle having its centre at (''a'',''b'') and radius ''r'' has the equation
-
{{Displayed math||<math>(x-a)^2 + (y-b)^2 = r^2\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>(x-a)^2 + (y-b)^2 = r^2\,\textrm{.}</math>}}

Version vom 08:48, 22. Okt. 2008

If the circle is to contain the point (-1,1), then that point's distance away from the centre (2,-1) must equal the circle's radius, r. Thus, we can obtain the circle's radius by calculating the distance between (-1,1) and (2,-1) using the distance formula,

\displaystyle \begin{align}

r &= \sqrt{(2-(-1))^2+(-1-1)^2} = \sqrt{3^2+(-2)^2} = \sqrt{9+4} = \sqrt{13}\,\textrm{.} \end{align}

When we know the circle's centre and its radius, we can write the equation of the circle,

\displaystyle (x-2)^2 + (y-(-1))^2 = (\sqrt{13})^{2}

which the same as

\displaystyle (x-2)^{2} + (y+1)^2 = 13\,\textrm{.}



Note: A circle having its centre at (a,b) and radius r has the equation

\displaystyle (x-a)^2 + (y-b)^2 = r^2\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.1:5b“