Lösung 2.3:8c
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 1: | Zeile 1: | ||
By completing the square, we can rewrite the function as | By completing the square, we can rewrite the function as | ||
| - | {{ | + | {{Abgesetzte Formel||<math>f(x) = x^{2}-6x+11 = (x-3)^{2} - 3^{2} + 11 = (x-3)^{2} + 2,</math>}} |
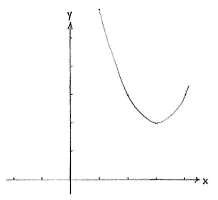
and when the function is written in this way, we see that the graph <math>y = (x-3)^{2} + 2</math> is the same curve as the parabola <math>y=x^{2}</math>, but shifted two units up and three units to the right (see sub-exercise a and b). | and when the function is written in this way, we see that the graph <math>y = (x-3)^{2} + 2</math> is the same curve as the parabola <math>y=x^{2}</math>, but shifted two units up and three units to the right (see sub-exercise a and b). | ||
Version vom 08:34, 22. Okt. 2008
By completing the square, we can rewrite the function as
| \displaystyle f(x) = x^{2}-6x+11 = (x-3)^{2} - 3^{2} + 11 = (x-3)^{2} + 2, |
and when the function is written in this way, we see that the graph \displaystyle y = (x-3)^{2} + 2 is the same curve as the parabola \displaystyle y=x^{2}, but shifted two units up and three units to the right (see sub-exercise a and b).
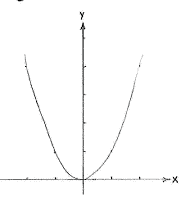
| The graph of f(x) = x² | The graph of f(x) = x² - 6x + 11 |