Lösung 2.2:6d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 1: | Zeile 1: | ||
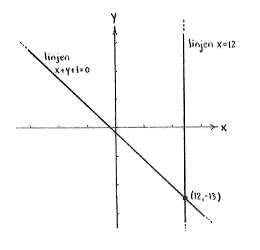
At the point where the lines cut each other, we have a point that lies on both lines and which must therefore satisfy the equations of both lines, | At the point where the lines cut each other, we have a point that lies on both lines and which must therefore satisfy the equations of both lines, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>x+y+1=0\qquad\text{and}\qquad x=12\,\textrm{.}</math>}} |
We obtain the solution to this system of equations by substituting <math>x=12</math> | We obtain the solution to this system of equations by substituting <math>x=12</math> | ||
into the first equation | into the first equation | ||
| - | {{ | + | {{Abgesetzte Formel||<math>12+y+1=0\quad\Leftrightarrow\quad y=-13\,\textrm{,}</math>}} |
which gives us the point of intersection as (12,-13). | which gives us the point of intersection as (12,-13). | ||
Version vom 08:29, 22. Okt. 2008
At the point where the lines cut each other, we have a point that lies on both lines and which must therefore satisfy the equations of both lines,
| \displaystyle x+y+1=0\qquad\text{and}\qquad x=12\,\textrm{.} |
We obtain the solution to this system of equations by substituting \displaystyle x=12 into the first equation
| \displaystyle 12+y+1=0\quad\Leftrightarrow\quad y=-13\,\textrm{,} |
which gives us the point of intersection as (12,-13).