Lösung 4.4:5b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
Let's first investigate when the equality
Let's first investigate when the equality
 +
{{Displayed math||<math>\tan u=\tan v</math>}}
-
<math>\tan u=\tan v</math>
+
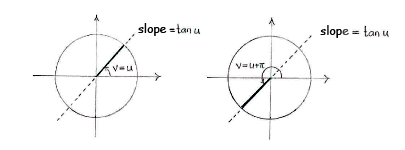
is satisfied. Because <math>\tan u</math> can be interpreted as the slope (gradient) of the line which makes an angle ''u'' with the positive ''x''-axis, we see that for a fixed value of <math>\tan u</math>, there are two angles ''v'' in the unit circle with this slope,
-
 
+
-
 
+
-
is satisfied. Because
+
-
<math>u</math>
+
-
can be interpreted as the slope (gradient) of the line which makes an angle
+
-
<math>u</math>
+
-
with the positive
+
-
<math>x</math>
+
-
-axis, we see that for a fixed value of tan u, there are two angles
+
-
<math>v</math>
+
-
in the unit circle with this slope:
+
-
 
+
-
 
+
-
<math>v=u</math>
+
-
and
+
-
<math>v=u+\pi </math>
+
 +
{{Displayed math||<math>v=u\qquad\text{and}\qquad v=u+\pi\,\textrm{.}</math>}}
[[Image:4_4_5_b.gif|center]]
[[Image:4_4_5_b.gif|center]]
-
slope
+
The angle ''v'' has the same slope after every half turn, so if we add multiples of
-
<math>=\text{ tan }u</math>
+
<math>\pi</math> to ''u'', we will obtain all the angles ''v'' which satisfy the equality
-
slope
+
-
<math>=\text{ tan }u</math>
+
 +
{{Displayed math||<math>v=u+n\pi\,,</math>}}
-
The angle
+
where ''n'' is an arbitrary integer.
-
<math>v</math>
+
-
has the same slope after every half turn, so if we add multiples of
+
-
<math>\pi \text{ }</math>
+
-
to
+
-
<math>u</math>, we will obtain all the angles
+
-
<math>v</math>
+
-
which satisfy the equality
+
-
 
+
-
 
+
-
<math>v=u+n\pi </math>
+
-
 
+
-
 
+
-
where
+
-
<math>n</math>
+
-
is an arbitrary integer.
+
If we apply this result to the equation
If we apply this result to the equation
-
 
+
{{Displayed math||<math>\tan x=\tan 4x</math>}}
-
<math>\tan x=\tan 4x</math>
+
-
 
+
we see that the solutions are given by
we see that the solutions are given by
 +
{{Displayed math||<math>4x = x+n\pi\qquad\text{(n is an arbitrary integer),}</math>}}
-
<math>4x=x+n\pi </math>
+
and solving for ''x'' gives
-
(
+
-
<math>n</math>
+
-
an arbitrary integer),
+
-
 
+
-
and solving for
+
-
<math>x</math>
+
-
gives
+
-
 
+
-
<math>x=\frac{1}{3}n\pi </math>
+
{{Displayed math||<math>x = \tfrac{1}{3}n\pi\qquad\text{(n is an arbitrary integer).}</math>}}
-
(
+
-
<math>n</math>
+
-
an arbitrary integer).
+

Version vom 14:02, 13. Okt. 2008

Let's first investigate when the equality

Vorlage:Displayed math

is satisfied. Because \displaystyle \tan u can be interpreted as the slope (gradient) of the line which makes an angle u with the positive x-axis, we see that for a fixed value of \displaystyle \tan u, there are two angles v in the unit circle with this slope,

Vorlage:Displayed math

The angle v has the same slope after every half turn, so if we add multiples of \displaystyle \pi to u, we will obtain all the angles v which satisfy the equality

Vorlage:Displayed math

where n is an arbitrary integer.

If we apply this result to the equation

Vorlage:Displayed math

we see that the solutions are given by

Vorlage:Displayed math

and solving for x gives

Vorlage:Displayed math

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:5b“