Lösung 4.4:3d

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
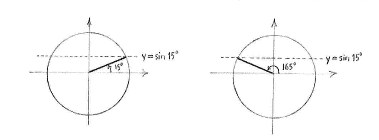
First, we observe from the unit circle that the equation has two solutions for
+
First, we observe from the unit circle that the equation has two solutions for <math>0^{\circ}\le 3x\le 360^{\circ}\,</math>,
-
<math>0^{\circ }\le \text{3}x\le \text{36}0^{\circ }</math>,
+
-
 
+
-
 
+
-
<math>3x=15^{\circ }</math>
+
-
and
+
-
<math>3x=180^{\circ }-15^{\circ }=165^{\circ }</math>
+
 +
{{Displayed math||<math>3x = 15^{\circ}\qquad\text{and}\qquad 3x = 180^{\circ} - 15^{\circ} = 165^{\circ}\,\textrm{.}</math>}}
[[Image:4_4_3_d.gif|center]]
[[Image:4_4_3_d.gif|center]]
Zeile 12: Zeile 7:
This means that all of the equation's solutions are
This means that all of the equation's solutions are
 +
{{Displayed math||<math>3x = 15^{\circ} + n\cdot 360^{\circ}\qquad\text{and}\qquad 3x = 165^{\circ} + n\cdot 360^{\circ}\,,</math>}}
-
<math>3x=15^{\circ }+n\centerdot 360^{\circ }</math>
+
for all integers ''n'', i.e.
-
and
+
-
<math>3x=165^{\circ }+n\centerdot 360^{\circ }</math>
+
-
 
+
-
 
+
-
for all integers
+
-
<math>n</math>, i.e.
+
-
 
+
-
<math>x=5^{\circ }+n\centerdot 120^{\circ }</math>
+
{{Displayed math||<math>x = 5^{\circ} + n\cdot 120^{\circ}\qquad\text{and}\qquad x = 55^{\circ} + n\cdot 120^{\circ}\,\textrm{.}</math>}}
-
and
+
-
<math>x=55^{\circ }+n\centerdot 120^{\circ }</math>
+

Version vom 13:02, 13. Okt. 2008

First, we observe from the unit circle that the equation has two solutions for \displaystyle 0^{\circ}\le 3x\le 360^{\circ}\,,

Vorlage:Displayed math

This means that all of the equation's solutions are

Vorlage:Displayed math

for all integers n, i.e.

Vorlage:Displayed math

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:3d“