Lösung 4.4:2b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
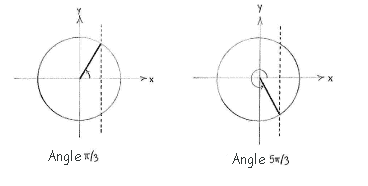
| - | The equation | + | The equation <math>\cos x= 1/2</math> has the solution <math>x=\pi/3</math> in the first quadrant, and the symmetric solution <math>x = 2\pi -\pi/3 = 5\pi/3</math> in the fourth quadrant. |
| - | <math>\cos x= | + | |
| - | has the solution | + | |
| - | <math>x= | + | |
| - | in the first quadrant, and the symmetric solution | + | |
| - | <math>x= | + | |
| - | in the fourth quadrant. | + | |
| - | + | ||
[[Image:4_4_2_b.gif|center]] | [[Image:4_4_2_b.gif|center]] | ||
| - | + | If we add multiples of <math>2\pi</math> to these two solutions, we obtain all the solutions | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | If we add multiples of | + | |
| - | <math>2\pi </math> | + | |
| - | to these two solutions, we obtain all the solutions | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>x = \frac{\pi}{3}+2n\pi\qquad\text{and}\qquad x = \frac{5\pi }{3}+2n\pi\,,</math>}} | ||
| - | where | + | where ''n'' is an arbitrary integer. |
| - | + | ||
| - | is an arbitrary integer. | + | |
Version vom 14:22, 10. Okt. 2008
The equation \displaystyle \cos x= 1/2 has the solution \displaystyle x=\pi/3 in the first quadrant, and the symmetric solution \displaystyle x = 2\pi -\pi/3 = 5\pi/3 in the fourth quadrant.
If we add multiples of \displaystyle 2\pi to these two solutions, we obtain all the solutions
where n is an arbitrary integer.