Lösung 4.4:1b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
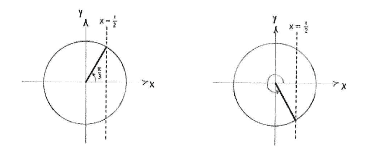
| - | The easiest angle to find is | + | The easiest angle to find is <math>v = \pi/3</math> in the first quadrant. When we draw the unit circle, we see that the angle which makes the same angle with the positive ''x''-axis as <math>v=\pi/3</math>, but is under the ''x''-axis, also has a cosine value of 1/2 (same ''x''-coordinate). |
| - | <math>v= | + | |
| - | in the first quadrant. When we draw the unit circle, we see that the angle which makes the same angle with the positive | + | |
| - | + | ||
| - | -axis as | + | |
| - | <math>v= | + | |
| - | + | ||
| - | -axis, also has a cosine value of | + | |
| - | + | ||
| - | (same | + | |
| - | + | ||
| - | -coordinate). | + | |
| - | + | ||
| - | + | ||
[[Image:4_4_1_b.gif|center]] | [[Image:4_4_1_b.gif|center]] | ||
| - | There are thus two angles, | + | There are thus two angles, <math>v=\pi/3</math> and <math>v=2\pi - \pi/3 = 5\pi/3</math> which have their cosine value equal to 1/2. |
| - | <math>v= | + | |
| - | and | + | |
| - | <math>v=2\pi - | + | |
| - | which have their cosine value equal to | + | |
| - | + | ||
Version vom 13:07, 10. Okt. 2008
The easiest angle to find is \displaystyle v = \pi/3 in the first quadrant. When we draw the unit circle, we see that the angle which makes the same angle with the positive x-axis as \displaystyle v=\pi/3, but is under the x-axis, also has a cosine value of 1/2 (same x-coordinate).
There are thus two angles, \displaystyle v=\pi/3 and \displaystyle v=2\pi - \pi/3 = 5\pi/3 which have their cosine value equal to 1/2.