Lösung 4.2:2a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K (Lösning 4.2:2a moved to Solution 4.2:2a: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
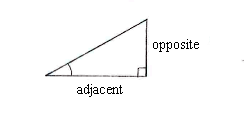
| - | {{ | + | The opposite and adjacent are given in the right-angled triangle and this means that the value of the tangent for the angle can be determined as the quotient between the opposite and the adjacent: |
| - | + | ||
| - | + | ||
| + | <math>\text{tan }v\text{ }={2}/{5}\;~</math> | ||
| + | |||
| + | |||
[[Image:4_2_2_a.gif|center]] | [[Image:4_2_2_a.gif|center]] | ||
| + | |||
| + | At the same time, this is a trigonometric equation for the angle | ||
| + | <math>v</math>. | ||
| + | |||
| + | NOTE: In the chapter on "Trigonometric equations", we will investigate more closely how to solve equations of this type. | ||
Version vom 09:09, 10. Okt. 2008
The opposite and adjacent are given in the right-angled triangle and this means that the value of the tangent for the angle can be determined as the quotient between the opposite and the adjacent:
\displaystyle \text{tan }v\text{ }={2}/{5}\;~
At the same time, this is a trigonometric equation for the angle \displaystyle v.
NOTE: In the chapter on "Trigonometric equations", we will investigate more closely how to solve equations of this type.