Lösung 4.3:3d

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
The expression for the angle
+
The expression for the angle <math>\pi/2 - v</math> differs from <math>\pi/2</math> by as much as <math>-v</math> differs from <math>0</math>. This means that <math>\pi/2-v</math> makes the same angle with the positive ''y''-axis as <math>-v</math> makes with the positive ''x''-axis.
-
<math>{\pi }/{2}\;-v</math>
+
-
differs from
+
-
<math>{\pi }/{2}\;</math>
+
-
by as much as
+
-
<math>-v\text{ }</math>
+
-
differs from
+
-
<math>0</math>. This means that
+
-
<math>{\pi }/{2}\;</math>
+
-
makes the same angle with the positive
+
-
<math>y</math>
+
-
-axis as
+
-
<math>-v\text{ }</math>
+
-
makes with the positive
+
-
<math>x</math>
+
-
-axis.
+
 +
{| align="center"
 +
| align="center" |[[Image:4_3_3_d-1.gif]]
 +
| width="20px"|&nbsp;
 +
| align="center" |[[Image:4_3_3_d-2.gif]]
 +
|-
 +
| align="center" |<small>Angle&nbsp;''v''</small>
 +
||
 +
| align="center" |<small>Angle&nbsp;π/2&nbsp;-&nbsp;''v''</small>
 +
|}
-
[[Image:4_3_3_d.gif|center]]
+
Therefore, the angle <math>\pi/2 - v</math> has a ''y''-coordinate which is equal to the ''x''-coordinate for the angle ''v'', i.e.
-
Angle
+
{{Displayed math||<math>\sin\Bigl(\frac{\pi}{2} - v\Bigr) = \cos v</math>}}
-
<math>v</math>
+
-
angle
+
-
<math>\pi -v</math>
+
-
+
-
Therefore, the angle
+
and from exercise c, we know that <math>\cos v = \sqrt{1-a^2}\,</math>,
-
<math>{\pi }/{2}\;-v</math>
+
-
has a
+
-
<math>y</math>
+
-
-coordinate which is equal to the
+
-
<math>x</math>
+
-
-coordinate for the angle
+
-
<math>v</math>, i.e.
+
-
 
+
{{Displayed math||<math>\sin\Bigl(\frac{\pi}{2}-v\Bigr) = \sqrt{1-a^2}\,\textrm{.}</math>}}
-
<math>\sin \left( {\pi }/{2}\;-v \right)=\cos v</math>
+
-
 
+
-
 
+
-
and from exercise c, we know that
+
-
<math>\cos v=\sqrt{1-a^{2}}</math>
+
-
 
+
-
 
+
-
 
+
-
<math>\sin \left( \frac{\pi }{2}-v \right)=\sqrt{1-a^{2}}</math>
+

Version vom 13:44, 9. Okt. 2008

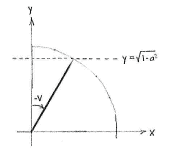
The expression for the angle \displaystyle \pi/2 - v differs from \displaystyle \pi/2 by as much as \displaystyle -v differs from \displaystyle 0. This means that \displaystyle \pi/2-v makes the same angle with the positive y-axis as \displaystyle -v makes with the positive x-axis.

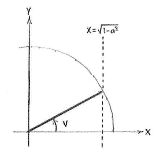
Image:4_3_3_d-1.gif   Image:4_3_3_d-2.gif
Angle v Angle π/2 - v

Therefore, the angle \displaystyle \pi/2 - v has a y-coordinate which is equal to the x-coordinate for the angle v, i.e.

Vorlage:Displayed math

and from exercise c, we know that \displaystyle \cos v = \sqrt{1-a^2}\,,

Vorlage:Displayed math

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.3:3d“