Lösung 4.2:4d
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
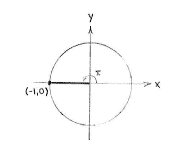
| - | If we use the unit circle and mark on the angle | + | If we use the unit circle and mark on the angle <math>\pi</math>, we see immediately that <math>\cos \pi = -1</math> and <math>\sin \pi = 0\,</math>. |
| - | <math>\pi </math>, we see immediately that | + | |
| - | <math>\ | + | |
| - | and | + | |
| - | <math>\ | + | |
[[Image:4_2_4_d.gif|center]] | [[Image:4_2_4_d.gif|center]] | ||
| Zeile 9: | Zeile 5: | ||
Thus, | Thus, | ||
| - | + | {{Displayed math||<math>\tan \pi =\frac{\sin \pi }{\cos \pi }=\frac{0}{-1}=0\,\textrm{.}</math>}} | |
| - | <math>\tan \pi =\frac{\sin \pi }{\cos \pi }=\frac{0}{-1}=0</math> | + | |
Version vom 10:37, 9. Okt. 2008
If we use the unit circle and mark on the angle \displaystyle \pi, we see immediately that \displaystyle \cos \pi = -1 and \displaystyle \sin \pi = 0\,.
Thus,