Lösung 4.2:4a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
| - | It can be a little difficult to draw the angle | + | It can be a little difficult to draw the angle <math>11\pi/6</math> straight onto a unit circle, but if we rewrite <math>11\pi/6</math> as |
| - | <math> | + | |
| - | straight onto a unit circle, but if we rewrite | + | |
| - | <math> | + | |
| - | + | ||
| - | as | + | |
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>\frac{11\pi}{6} = \frac{6\pi+3\pi+2\pi}{6} = \pi + \frac{\pi}{2} + \frac{\pi}{3}</math>}} | ||
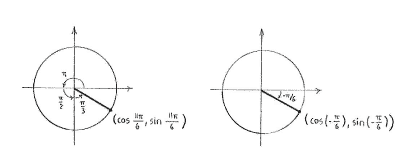
we see that we have an angle that lies in the fourth quadrant, as in the figure below to the left. | we see that we have an angle that lies in the fourth quadrant, as in the figure below to the left. | ||
| - | We also note that this angle corresponds to exactly the same point on the unit circle as the angle | + | We also note that this angle corresponds to exactly the same point on the unit circle as the angle <math>-\pi/6</math>, and because we calculated <math>\cos (-\pi/6)</math> in exercise 4.2:3f, we have that |
| - | <math>- | + | |
| - | <math>\cos | + | |
| - | in exercise | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>\cos\frac{11\pi}{6} = \cos\Bigl(-\frac{\pi}{6}\Bigr) = \frac{\sqrt{3}}{2}\,\textrm{.}</math>}} | ||
[[Image:4_2_4_a.gif|center]] | [[Image:4_2_4_a.gif|center]] | ||
Version vom 08:27, 9. Okt. 2008
It can be a little difficult to draw the angle \displaystyle 11\pi/6 straight onto a unit circle, but if we rewrite \displaystyle 11\pi/6 as
we see that we have an angle that lies in the fourth quadrant, as in the figure below to the left.
We also note that this angle corresponds to exactly the same point on the unit circle as the angle \displaystyle -\pi/6, and because we calculated \displaystyle \cos (-\pi/6) in exercise 4.2:3f, we have that