Lösung 4.2:3b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
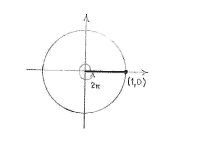
| - | The angle | + | The angle <math>2\pi</math> corresponds to a whole revolution and therefore we see that if we draw in a line with angle <math>2\pi</math> relative to the positive ''x''-axis, we will get the positive ''x''-axis. |
| - | <math> | + | |
| - | corresponds to a whole revolution and therefore we see that if we draw in a line with angle | + | |
| - | <math> | + | |
| - | relative to the positive | + | |
| - | + | ||
| - | -axis, we will get the positive | + | |
| - | + | ||
| - | -axis. | + | |
[[Image:4_2_3_b.gif|center]] | [[Image:4_2_3_b.gif|center]] | ||
| - | Because | + | Because <math>\cos 2\pi</math> is the ''x''-coordinate for the point of intersection between the line with angle <math>2\pi</math> and the unit circle, we can see directly that <math>\cos 2\pi = 1\,</math>. |
| - | <math>\cos | + | |
| - | is the | + | |
| - | + | ||
| - | -coordinate for the point of intersection between the line with angle | + | |
| - | <math> | + | |
| - | and the unit circle, we can see directly that | + | |
| - | <math>\cos | + | |
Version vom 07:48, 9. Okt. 2008
The angle \displaystyle 2\pi corresponds to a whole revolution and therefore we see that if we draw in a line with angle \displaystyle 2\pi relative to the positive x-axis, we will get the positive x-axis.
Because \displaystyle \cos 2\pi is the x-coordinate for the point of intersection between the line with angle \displaystyle 2\pi and the unit circle, we can see directly that \displaystyle \cos 2\pi = 1\,.