Lösung 4.2:1c
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
| - | [[Image:4_2_1_c.gif|center]] | ||
| - | |||
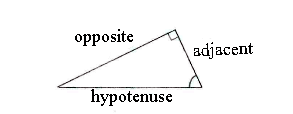
The difficulty is to recognize the sides in the right-angled triangle. A simple rule of thumb is that the hypotenuse is the side which is opposite the right angle (it is also the longest side in the triangle). The adjacent is the side which lies near to the angle that we are considering and the opposite is the third side. | The difficulty is to recognize the sides in the right-angled triangle. A simple rule of thumb is that the hypotenuse is the side which is opposite the right angle (it is also the longest side in the triangle). The adjacent is the side which lies near to the angle that we are considering and the opposite is the third side. | ||
| - | + | [[Image:4_2_1_c.gif|center]] | |
| - | The opposite is given, whilst it is the adjacent that we are looking for. The | + | The opposite is given, whilst it is the adjacent that we are looking for. The tangent of the angle is given by |
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>\tan 40^{\circ } = \frac{14}{x}</math>}} | ||
and thus | and thus | ||
| - | + | {{Displayed math||<math>x = \frac{14}{\tan 40^{\circ }}\quad \left( \approx 16\textrm{.}7 \right)\,\textrm{.}</math>}} | |
| - | <math>x=\frac{14}{\tan 40^{\circ }}\quad \left( \approx 16.7 \right)</math> | + | |
Version vom 14:05, 8. Okt. 2008
The difficulty is to recognize the sides in the right-angled triangle. A simple rule of thumb is that the hypotenuse is the side which is opposite the right angle (it is also the longest side in the triangle). The adjacent is the side which lies near to the angle that we are considering and the opposite is the third side.
The opposite is given, whilst it is the adjacent that we are looking for. The tangent of the angle is given by
and thus