Lösung 4.2:1b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
[[Image:4_2_1_b.gif|center]]
 
- 
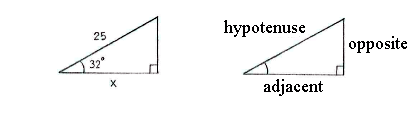
If we reflect the triangle, it can be easier to identify the different sides in the triangle.
If we reflect the triangle, it can be easier to identify the different sides in the triangle.
 +
[[Image:4_2_1_b.gif|center]]
 +
Because we know the hypotenuse and want to find the adjacent, it is appropriate to consider to the quotient for the cosine of an angle,
-
Because we know the hypotenuse and want to find the adjacent, it is appropriate to consider to the quotient for the cosine of an angle:
+
{{Displayed math||<math>\cos 32 = \frac{x}{25}\quad \Bigl({}=\frac{\text{adjacent}}{\text{hypotenuse }}\Bigr)\,\textrm{.}</math>}}
-
 
+
-
 
+
-
<math>\cos 32=\frac{x}{25}\quad \left( =\frac{\text{adjacent}}{\text{hypotenuse }} \right)</math>
+
-
 
+
-
 
+
-
From this equation, we can solve for
+
-
<math>x</math>:
+
 +
From this equation, we can solve for ''x'',
-
<math>x=25\centerdot \cos 32\quad \left( \approx 21.2 \right)</math>
+
{{Displayed math||<math>x = 25\cdot \cos 32\quad ({}\approx 21\textrm{.}2)\,\textrm{.}</math>}}

Version vom 14:00, 8. Okt. 2008

If we reflect the triangle, it can be easier to identify the different sides in the triangle.

Because we know the hypotenuse and want to find the adjacent, it is appropriate to consider to the quotient for the cosine of an angle,

Vorlage:Displayed math

From this equation, we can solve for x,

Vorlage:Displayed math

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:1b“