Aus Online Mathematik Brückenkurs 1

Version vom 12:06, 27. Sep. 2008 (bearbeiten) Ian (Diskussion | Beiträge) ← Zum vorherigen Versionsunterschied		Version vom 11:31, 8. Okt. 2008 (bearbeiten) (rückgängig) Tek (Diskussion | Beiträge) K Zum nächsten Versionsunterschied →
Zeile 1:		Zeile 1:
-	By completing the square, we can rewrite the	+	By completing the square, we can rewrite the ''x''- and ''y''-terms as quadratic expressions,
-	<math>x</math>	+
-	- and	+
-	<math>y</math>	+
-	-terms as quadratic expressions,	+
-		+	{{Displayed math||<math>\begin{align}
-	<math>x^{2}-2x=\left( x-1 \right)^{2}-1^{2}</math>	+	x^2 - 2x &= (x-1)^2 - 1^2\,,\\[5pt]
-		+	y^2 + 6y &= (y+3)^2 - 3^2\,,
-		+	\end{align}</math>}}
-	<math>y^{2}+6y=\left( y+3 \right)^{2}-3^{2}</math>	+
	and the whole equation then has standard form,		and the whole equation then has standard form,
		+	{{Displayed math||<math>\begin{align}
		+	(x-1)^2 - 1 + (y+3)^2 - 9 &= -3\,,\\[5pt]
		+	(x-1)^2 + (y+3)^2 &= 7\,\textrm{.}
		+	\end{align}</math>}}
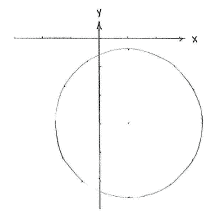
-	<math>\begin{align}	+	From this, we see that the circle has its centre at (1,-3) and radius <math>\sqrt{7}\,</math>.
-	& \left( x-1 \right)^{2}-1+\left( y+3 \right)^{2}-9=-3 \\	+
-	& \Leftrightarrow \quad \left( x-1 \right)^{2}+\left( y+3 \right)^{2}=7 \\	+
-	\end{align}</math>	+
-
-	From this, we see that the circle has its centre at
-	<math>\left( 1 \right.,\left. -3 \right)</math>
-	and radius
-	<math>\sqrt{7}</math>.
-
-
-	{{NAVCONTENT_START}}
	<center> [[Image:4_1_7_c.gif]] </center>		<center> [[Image:4_1_7_c.gif]] </center>
-
-	{{NAVCONTENT_STOP}}

---

Version vom 11:31, 8. Okt. 2008

By completing the square, we can rewrite the x- and y-terms as quadratic expressions,

Vorlage:Displayed math

and the whole equation then has standard form,

Vorlage:Displayed math

From this, we see that the circle has its centre at (1,-3) and radius \displaystyle \sqrt{7}\,.