Lösung 4.1:7b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
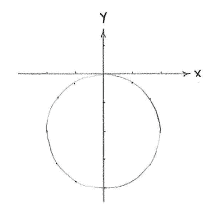
The equation is almost in the standard form for a circle; all that is needed is for us to collect together the
+
The equation is almost in the standard form for a circle; all that is needed is for us to collect together the ''y''²- and ''y''-terms into a quadratic term by completing the square
-
<math>y^{\text{2}}</math>
+
-
- and
+
-
<math>y</math>
+
-
-terms into a quadratic term by completing the square
+
-
 
+
-
 
+
-
<math>y^{2}+4y=\left( y+2 \right)^{2}-2^{2}</math>
+
 +
{{Displayed math||<math>y^2 + 4y = (y+2)^2 - 2^2\,\textrm{.}</math>}}
After rewriting, the equation is
After rewriting, the equation is
 +
{{Displayed math||<math>x^2 + (y+2)^2 = 4</math>}}
-
<math>x^{2}+\left( y+2 \right)^{2}=4</math>
+
and we see that the equation describes a circle having its centre at (0,-2) and radius <math>\sqrt{4}=2\,</math>.
-
and we see that the equation describes a circle having its centre at
 
-
<math>\left( 0 \right.,\left. -2 \right)</math>
 
-
and radius
 
-
<math>\sqrt{4}=2</math>.
 
- 
- 
-
{{NAVCONTENT_START}}
 
<center> [[Image:4_1_7_b.gif]] </center>
<center> [[Image:4_1_7_b.gif]] </center>
- 
- 
-
{{NAVCONTENT_STOP}}
 

Version vom 11:23, 8. Okt. 2008

The equation is almost in the standard form for a circle; all that is needed is for us to collect together the y²- and y-terms into a quadratic term by completing the square

Vorlage:Displayed math

After rewriting, the equation is

Vorlage:Displayed math

and we see that the equation describes a circle having its centre at (0,-2) and radius \displaystyle \sqrt{4}=2\,.


Image:4_1_7_b.gif
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.1:7b“