Lösung 4.1:7a
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
| - | As the equation stands, it is difficult directly to know anything about the circle, but if we complete the square and combine | + | As the equation stands, it is difficult directly to know anything about the circle, but if we complete the square and combine ''x''- and ''y''-terms together in their own respective square terms, then we will have the equation in the standard form |
| - | + | ||
| - | - and | + | |
| - | + | ||
| - | - terms together in their own respective square terms, then we will have the equation in the standard form | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>(x-a)^2 + (y-b)^2 = r^2\,,</math>}} | ||
and we will then be able to read off the circle's centre and radius. | and we will then be able to read off the circle's centre and radius. | ||
| - | If we take the | + | If we take the ''x''- and ''y''-terms on the left-hand side and complete the square, we get |
| - | + | ||
| - | - and | + | |
| - | + | ||
| - | - terms on the left-hand side and complete the square, we get | + | |
| - | + | {{Displayed math||<math>\begin{align} | |
| - | <math>x^ | + | x^2 + 2x &= (x+1)^2-1^2\,,\\[5pt] |
| - | + | y^2 - 2y &= (y-1)^2-1^2\,, | |
| - | + | \end{align}</math>}} | |
| - | + | ||
and then the whole equation can be written as | and then the whole equation can be written as | ||
| - | + | {{Displayed math||<math>(x+1)^2 - 1^2 + (y-1)^2 - 1^2 = 1\,,</math>}} | |
| - | <math> | + | |
| - | + | ||
or, with the constants moved to the right-hand side, | or, with the constants moved to the right-hand side, | ||
| + | {{Displayed math||<math>(x+1)^2 + (y-1)^2 = 3\,\textrm{.}</math>}} | ||
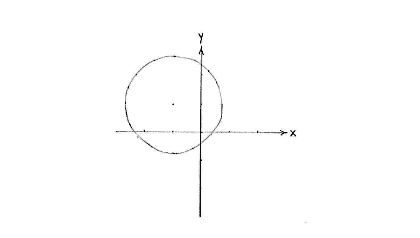
| - | <math>\ | + | This is a circle having its centre at (-1,1) and radius <math>\sqrt{3}\,</math>. |
| - | + | ||
| - | This is a circle having its centre at | ||
| - | <math>\left( -1 \right.,\left. 1 \right)</math> | ||
| - | and radius | ||
| - | <math>\sqrt{3}</math>. | ||
| - | {{NAVCONTENT_START}} | ||
<center> [[Image:4_1_7a-2(2).gif]] </center> | <center> [[Image:4_1_7a-2(2).gif]] </center> | ||
| - | {{NAVCONTENT_STOP}} | ||
Version vom 11:19, 8. Okt. 2008
As the equation stands, it is difficult directly to know anything about the circle, but if we complete the square and combine x- and y-terms together in their own respective square terms, then we will have the equation in the standard form
and we will then be able to read off the circle's centre and radius.
If we take the x- and y-terms on the left-hand side and complete the square, we get
and then the whole equation can be written as
or, with the constants moved to the right-hand side,
This is a circle having its centre at (-1,1) and radius \displaystyle \sqrt{3}\,.