Lösung 4.4:3c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.4:3c moved to Solution 4.4:3c: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
If we consider the entire expression
-
<center> [[Image:4_4_3c.gif]] </center>
+
<math>x+\text{4}0^{\circ }</math>
-
{{NAVCONTENT_STOP}}
+
as an unknown, we have a fundamental trigonometric equation and can, with the aid of the unit circle, see that there are two solutions to the equation for
 +
<math>0^{\circ }\le x+\text{4}0^{\circ }\le \text{36}0^{\circ }</math>
 +
namely
 +
<math>x+\text{4}0^{\circ }=\text{65}^{\circ }</math>
 +
and the symmetric solution
 +
<math>x+\text{4}0^{\circ }=\text{18}0^{\circ }-\text{65}^{\circ }=\text{115}^{\circ }</math>.
[[Image:4_4_3_c.gif|center]]
[[Image:4_4_3_c.gif|center]]
 +
 +
It is then easy to set up the general solution by adding multiples of
 +
<math>360^{\circ }</math>,
 +
 +
 +
<math>x+\text{4}0^{\circ }=\text{65}^{\circ }+n\centerdot 360^{\circ }</math>
 +
and
 +
<math>x+\text{4}0^{\circ }=\text{115}^{\circ }+n\centerdot 360^{\circ }</math>
 +
 +
 +
for all integers
 +
<math>n</math>, which gives
 +
 +
 +
<math>x=2\text{5}^{\circ }+n\centerdot 360^{\circ }</math>
 +
and
 +
<math>x=7\text{5}^{\circ }+n\centerdot 360^{\circ }</math>

Version vom 09:50, 1. Okt. 2008

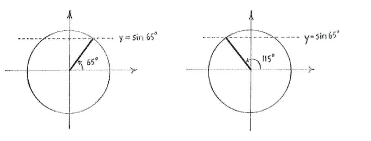
If we consider the entire expression \displaystyle x+\text{4}0^{\circ } as an unknown, we have a fundamental trigonometric equation and can, with the aid of the unit circle, see that there are two solutions to the equation for \displaystyle 0^{\circ }\le x+\text{4}0^{\circ }\le \text{36}0^{\circ } namely \displaystyle x+\text{4}0^{\circ }=\text{65}^{\circ } and the symmetric solution \displaystyle x+\text{4}0^{\circ }=\text{18}0^{\circ }-\text{65}^{\circ }=\text{115}^{\circ }.


It is then easy to set up the general solution by adding multiples of \displaystyle 360^{\circ },


\displaystyle x+\text{4}0^{\circ }=\text{65}^{\circ }+n\centerdot 360^{\circ } and \displaystyle x+\text{4}0^{\circ }=\text{115}^{\circ }+n\centerdot 360^{\circ }


for all integers \displaystyle n, which gives


\displaystyle x=2\text{5}^{\circ }+n\centerdot 360^{\circ } and \displaystyle x=7\text{5}^{\circ }+n\centerdot 360^{\circ }

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.4:3c“