Lösung 4.2:3e

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 4.2:3e moved to Solution 4.2:3e: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
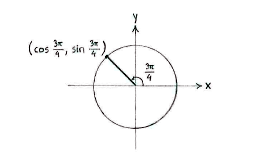
If we draw the line which has angle
-
<center> [[Image:4_2_3e-1(2).gif]] </center>
+
<math>\text{3}{\pi }/{4}\;</math>
-
{{NAVCONTENT_STOP}}
+
relative to the positive
-
{{NAVCONTENT_START}}
+
<math>x</math>
-
<center> [[Image:4_2_3e-2(2).gif]] </center>
+
-axis, it will cut the unit circle in the second quadrant.
-
{{NAVCONTENT_STOP}}
+
[[Image:4_2_3_e1.gif|center]]
[[Image:4_2_3_e1.gif|center]]
 +
At first sight, the figure gives information about the signs of
 +
<math>\cos {3\pi }/{4}\;</math>
 +
and
 +
<math>\sin {3\pi }/{4}\;</math>: cosine, which is the
 +
<math>x</math>
 +
-coordinate for the intersection point, is negative, whereas sine, which is the
 +
<math>y</math>
 +
-coordinate for the intersection point, is positive.
 +
 +
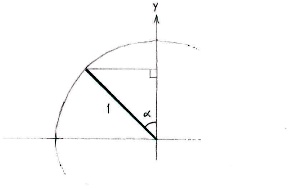
In order to go further and determine the coordinates of the intersection points, we concentrate on the second quadrant and introduce an auxiliary triangle which has the line associated with the angle as the hypotenuse and its other edges parallel to the coordinate axes.
 +
 +
[[Image:4_2_3_e_2.gif|center]]
[[Image:4_2_3_e_2.gif|center]]
 +
 +
In this triangle, we see that the angle
 +
<math>\alpha </math>
 +
between the hypotenuse and the
 +
<math>y</math>
 +
-axis is the part of the
 +
<math>y</math>
 +
-axis that lies in the second quadrant, i.e.
 +
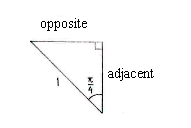
<math>\alpha =\frac{3\pi }{4}-\frac{\pi }{2}=\frac{\pi }{4}</math>. With the help of trigonometry, we can now determine the triangle's sides.
 +
 +
 +
[[Image:4_2_3_e3.gif|center]]
[[Image:4_2_3_e3.gif|center]]
 +
 +
This shows that the intersection point has coordinates
 +
<math>\left( -\frac{1}{\sqrt{2}} \right.,\left. \frac{1}{\sqrt{2}} \right)</math>
 +
(note the minus sign in the
 +
<math>x</math>
 +
-coordinate) and therefore that
 +
<math>\sin \frac{3\pi }{4}=\frac{1}{\sqrt{2}}</math>.

Version vom 12:25, 28. Sep. 2008

If we draw the line which has angle \displaystyle \text{3}{\pi }/{4}\; relative to the positive \displaystyle x -axis, it will cut the unit circle in the second quadrant.

At first sight, the figure gives information about the signs of \displaystyle \cos {3\pi }/{4}\; and \displaystyle \sin {3\pi }/{4}\;: cosine, which is the \displaystyle x -coordinate for the intersection point, is negative, whereas sine, which is the \displaystyle y -coordinate for the intersection point, is positive.

In order to go further and determine the coordinates of the intersection points, we concentrate on the second quadrant and introduce an auxiliary triangle which has the line associated with the angle as the hypotenuse and its other edges parallel to the coordinate axes.


In this triangle, we see that the angle \displaystyle \alpha between the hypotenuse and the \displaystyle y -axis is the part of the \displaystyle y -axis that lies in the second quadrant, i.e. \displaystyle \alpha =\frac{3\pi }{4}-\frac{\pi }{2}=\frac{\pi }{4}. With the help of trigonometry, we can now determine the triangle's sides.


This shows that the intersection point has coordinates \displaystyle \left( -\frac{1}{\sqrt{2}} \right.,\left. \frac{1}{\sqrt{2}} \right) (note the minus sign in the \displaystyle x -coordinate) and therefore that \displaystyle \sin \frac{3\pi }{4}=\frac{1}{\sqrt{2}}.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_4.2:3e“