Lösung 4.1:6c
Aus Online Mathematik Brückenkurs 1
K (Lösning 4.1:6c moved to Solution 4.1:6c: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | {{ | + | What we need to do is to rewrite the equation in the standard form |
| - | < | + | |
| - | {{ | + | |
| + | <math>\left( x-a \right)^{2}+\left( y-b \right)^{2}=r^{2}</math> | ||
| + | |||
| + | |||
| + | because then we can read off the circle's centre | ||
| + | <math>\left( a \right.,\left. b \right)</math> | ||
| + | and radius, | ||
| + | <math>r</math>. | ||
| + | |||
| + | In our case, we need only take out the factor | ||
| + | <math>~\text{3}</math> | ||
| + | from the brackets on the left-hand side | ||
| + | |||
| + | |||
| + | <math>\begin{align} | ||
| + | & \left( 3x-1 \right)^{2}+\left( 3y+7 \right)^{2}=3^{2}\left( x-\frac{1}{3} \right)^{2}+3^{2}\left( y+\frac{7}{3} \right)^{2} \\ | ||
| + | & =9\left( x-\frac{1}{3} \right)^{2}+9\left( y+\frac{7}{3} \right)^{2} \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | |||
| + | and then divide both sides by | ||
| + | <math>\text{9}</math> | ||
| + | , so as to get the equation in the desired form: | ||
| + | |||
| + | |||
| + | <math>\left( x-\frac{1}{3} \right)^{2}+\left( y+\frac{7}{3} \right)^{2}=\frac{10}{9}</math> | ||
| + | |||
| + | Because the right-hand side can be written as | ||
| + | <math>\left( \sqrt{\frac{10}{9}} \right)^{2}</math> | ||
| + | and the term | ||
| + | <math>\left( y+\frac{7}{3} \right)^{2}</math> | ||
| + | as | ||
| + | <math></math> | ||
| + | |||
| + | <math>\left( y-\left( -\frac{7}{3} \right) \right)^{2}</math>, the equation describes a circle with its centre at | ||
| + | <math>\left( \frac{1}{3} \right.,\left. -\frac{7}{3} \right)</math> | ||
| + | and radius | ||
| + | <math>\sqrt{\frac{10}{9}}=\frac{\sqrt{10}}{3}</math> | ||
| + | |||
{{NAVCONTENT_START}} | {{NAVCONTENT_START}} | ||
<center> [[Image:4_1_6c-2(2).gif]] </center> | <center> [[Image:4_1_6c-2(2).gif]] </center> | ||
{{NAVCONTENT_STOP}} | {{NAVCONTENT_STOP}} | ||
Version vom 11:45, 27. Sep. 2008
What we need to do is to rewrite the equation in the standard form
\displaystyle \left( x-a \right)^{2}+\left( y-b \right)^{2}=r^{2}
because then we can read off the circle's centre
\displaystyle \left( a \right.,\left. b \right)
and radius,
\displaystyle r.
In our case, we need only take out the factor \displaystyle ~\text{3} from the brackets on the left-hand side
\displaystyle \begin{align}
& \left( 3x-1 \right)^{2}+\left( 3y+7 \right)^{2}=3^{2}\left( x-\frac{1}{3} \right)^{2}+3^{2}\left( y+\frac{7}{3} \right)^{2} \\
& =9\left( x-\frac{1}{3} \right)^{2}+9\left( y+\frac{7}{3} \right)^{2} \\
\end{align}
and then divide both sides by
\displaystyle \text{9}
, so as to get the equation in the desired form:
\displaystyle \left( x-\frac{1}{3} \right)^{2}+\left( y+\frac{7}{3} \right)^{2}=\frac{10}{9}
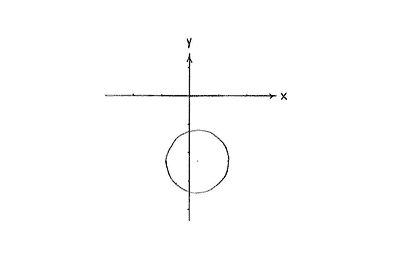
Because the right-hand side can be written as \displaystyle \left( \sqrt{\frac{10}{9}} \right)^{2} and the term \displaystyle \left( y+\frac{7}{3} \right)^{2} as \displaystyle
\displaystyle \left( y-\left( -\frac{7}{3} \right) \right)^{2}, the equation describes a circle with its centre at \displaystyle \left( \frac{1}{3} \right.,\left. -\frac{7}{3} \right) and radius \displaystyle \sqrt{\frac{10}{9}}=\frac{\sqrt{10}}{3}