Lösung 2.2:9c

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
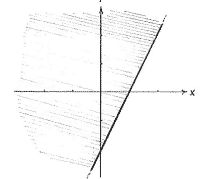
First, we draw the regions which the various inequalities define.
First, we draw the regions which the various inequalities define.
-
[[Image:2_2_9_c-1(5)_1.gif|center]]
 
-
[[Image:2_2_9_c-1(5)_2.gif|center]]
+
{| align="center"
 +
||[[Image:2_2_9_c-1(5)_1.gif|center]]
 +
||[[Image:2_2_9_c-1(5)_2.gif|center]]
 +
|-
 +
||<small>The region ''x''&nbsp;+&nbsp;''y''&nbsp;≥&nbsp;-2</small>
 +
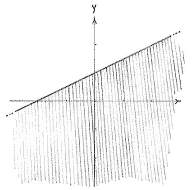
||<small>The region 2''x''&nbsp;-&nbsp;''y''&nbsp;≤&nbsp;2</small>
 +
|-
 +
||[[Image:2_2_9_c-1(5)_3.gif|center]]
 +
|-
 +
||<small>The region 2''y''&nbsp;-&nbsp;''x''&nbsp;≤&nbsp;2</small>
 +
|}
-
[[Image:2_2_9_c-1(5)_3.gif|center]]
 
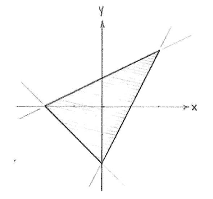
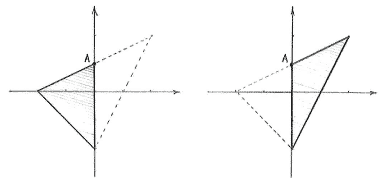
The triangle is defined as those points which satisfy all inequalities, which is the region which the three grey areas have in common.
The triangle is defined as those points which satisfy all inequalities, which is the region which the three grey areas have in common.
 +
[[Image:2_2_9_c-2(5).gif|center]]
[[Image:2_2_9_c-2(5).gif|center]]
 +
Before we start thinking about how we should calculate the area of the triangle, we must determine the corner points of the triangle.
Before we start thinking about how we should calculate the area of the triangle, we must determine the corner points of the triangle.
-
If we write equations for the edges in pairs,
+
If we write equations for the edges in pairs
 +
{{Displayed math||<math>(1)\ \left\{\begin{align} x+y&=-2,\\ 2x-y&=2,\end{align}\right.\qquad
 +
(2)\ \left\{\begin{align} x+y &= -2,\\ -x+2y &= 2,\end{align}\right.\qquad
 +
\text{and}\qquad
 +
(3)\ \left\{\begin{align} 2x-y &= 2,\\ -x+2y &= 2,\end{align}\right.</math>}}
-
<math>\left( 1 \right)\left\{ \begin{matrix}
+
we obtain an equation system which determines the points of intersections between respective pairs of lines, and these points correspond to the triangle's corners.
-
x+y=-2 \\
+
-
2x-y=2 \\
+
-
\end{matrix} \right.</math>
+
-
+
-
<math>\left( 2 \right)\left\{ \begin{matrix}
+
-
x+y=-2 \\
+
-
-x+2y=2 \\
+
-
\end{matrix} \right.</math>
+
-
+
-
<math>\left( 3 \right)\left\{ \begin{matrix}
+
-
2x-y=2 \\
+
-
-x+2y=2 \\
+
-
\end{matrix} \right.</math>
+
 +
<ol>
 +
<li>We can solve the first system by summing the two equations:
 +
{| align="center" style="padding:10px 0px 10px 0px;"
 +
||
 +
|align="right"|<math>x</math>
 +
||<math>{}+{}</math>
 +
|align="right"|<math>y</math>
 +
||<math>{}={}</math>
 +
|align="right"|<math>-2</math>
 +
|-
 +
|align="left"|<math>+\ \ </math>
 +
|align="right"|<math>2x</math>
 +
||<math>{}-{}</math>
 +
||<math>y</math>
 +
||<math>{}={}</math>
 +
|align="right"|<math>2</math>
 +
|-
 +
|colspan="6"|<hr>
 +
|-
 +
||
 +
|align="right"|<math>3x</math>
 +
||
 +
||
 +
||<math>{}={}</math>
 +
|align="right"|<math>0</math>
 +
|}
 +
 +
Thus, we obtain <math>x=0</math> and, from the equation <math>x+y=-2</math>, that <math>y=-2</math>.
 +
</ol>
-
we obtain an equation system which determines the points of intersections between respective pairs of lines, and these points correspond to the triangle's corners.
 
-
1) We can solve the first system by summing the two equations:
 
-
<math>\begin{align}
 
-
& \begin{matrix}
 
-
{} & x & + & y & = & -2 \\
 
-
+ & 2x & - & y & = & 2 \\
 
-
- & - & - & - & - & - \\
 
-
{} & 3x & {} & {} & = & 0 \\
 
-
\end{matrix} \\
 
-
& \\
 
-
\end{align}</math>
 
-
Thus, we obtain
 
-
<math>x=0\text{ }</math>
 
-
and, from the equation
 
-
<math>x+y=-\text{2}</math>, that
 
-
<math>y=-\text{2}</math>.
 
2) In the same way, we sum the equations in the second system,
2) In the same way, we sum the equations in the second system,

Version vom 14:37, 24. Sep. 2008

First, we draw the regions which the various inequalities define.

The region x + y ≥ -2 The region 2x - y ≤ 2
The region 2y - x ≤ 2

The triangle is defined as those points which satisfy all inequalities, which is the region which the three grey areas have in common.



Before we start thinking about how we should calculate the area of the triangle, we must determine the corner points of the triangle.

If we write equations for the edges in pairs

Vorlage:Displayed math

we obtain an equation system which determines the points of intersections between respective pairs of lines, and these points correspond to the triangle's corners.

  1. We can solve the first system by summing the two equations:
    \displaystyle x \displaystyle {}+{} \displaystyle y \displaystyle {}={} \displaystyle -2
    \displaystyle +\ \ \displaystyle 2x \displaystyle {}-{} \displaystyle y \displaystyle {}={} \displaystyle 2
    \displaystyle 3x \displaystyle {}={} \displaystyle 0

    Thus, we obtain \displaystyle x=0 and, from the equation \displaystyle x+y=-2, that \displaystyle y=-2.




2) In the same way, we sum the equations in the second system,


\displaystyle \begin{align} & \begin{matrix} {} & x & + & y & = & -2 \\ + & -x & + & 2y & = & 2 \\ - & - & - & - & - & - \\ {} & {} & 3y & {} & = & 0 \\ \end{matrix} \\ & \\ \end{align}

which gives \displaystyle y=0 and \displaystyle x=-\text{2}.

3) The final equation system is a little trickier to solve, but if we make \displaystyle y the subject in the first equation, so that \displaystyle y=\text{2}x-\text{2}, and substitute it into the second equation, we get


\displaystyle -x+\left( 2x-2 \right)\ \Leftrightarrow \ 3x-4=2\ \Leftrightarrow \ x=2


The corresponding value for \displaystyle y is \displaystyle y=\text{2}\centerdot \text{2-2}=\text{2}.

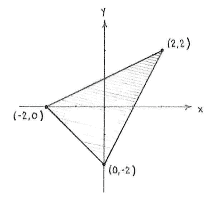
The triangle's corner points are thus \displaystyle \left( 0,-\text{2} \right), \displaystyle \left( -\text{2},0 \right) and \displaystyle \left( \text{2},\text{2} \right).

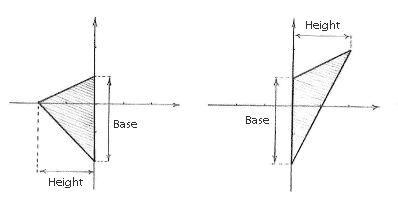
The problem we have in calculating the area of the triangle with the formula

Area= \displaystyle \frac{1}{2} (base)∙(height)

is that there is no natural base for the triangle, since none of the edges are parallel with any of the coordinate axes. On the other hand, what we can do is to divide up the triangle along the \displaystyle y -axis and obtain two sub-triangles where we use the \displaystyle y -axis as the base.


This division creates a new corner point for the triangles (marked A in the figure above) and we can determine it to be the intersection point between the line \displaystyle 2y-x=\text{2 } and the \displaystyle y -axis


\displaystyle \left\{ \begin{matrix} 2y-x=\text{2 } \\ \quad x=0 \\ \end{matrix} \right.


which gives that the new corner point is at \displaystyle \left( 0,\text{1} \right).

We now have all the information we need for calculating the base, height and area of the two sub-triangles.


Finally, it remains only to add up the sub-areas to get the total area of the triangle:

Area \displaystyle =\text{3}+\text{3}=\text{6}.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:9c“