Lösung 2.2:8b

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
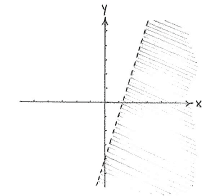
A point whose coordinates satisfy
+
A point whose coordinates satisfy <math>y < 3x-4</math> has a ''y''-coordinate which is less than that of a point lying on the line <math>y=3x-4</math> and having the same ''x''-coordinate. This means that the area we should shade consists of all points below the line <math>y=3x-4</math>.
-
<math>y<3x-4</math>
+
-
has a
+
-
<math>y</math>
+
-
-coordinate which is less than that of a point lying on the line
+
-
<math>y=3x-4</math>
+
-
and having the same
+
-
<math>x</math>
+
-
-coordinate. This means that the area we should shade consists of all points below the line
+
-
<math>y=3x-4</math>.
+
-
{{NAVCONTENT_START}}
 
-
{{NAVCONTENT_STOP}}
 
[[Image:2_2_8_b.gif|center]]
[[Image:2_2_8_b.gif|center]]
-
We can draw the line
+
 
-
<math>y=3x-4</math>
+
We can draw the line <math>y=3x-4</math> by choosing two ''x''-values, for example
-
by choosing two x-values, for example
+
<math>x=0</math> and <math>x=1</math>, using the equation of the line to calculate the corresponding ''y''-coordinates, <math>y=3\cdot 0-4=-4</math> and <math>y=3\cdot 1-4=-1</math> respectively, and then draw a straight line between the two points that we have obtained.
-
<math>x=0</math>
+
-
and
+
-
<math>x=1</math>, using the equation of the line to calculate the corresponding y-coordinates,
+
-
<math>y=3\centerdot 0-4=-4</math>
+
-
and
+
-
<math>y=3\centerdot 1-4=-1</math>
+
-
respectively, and then draw a straight line between the two points that we have obtained.
+

Version vom 13:44, 24. Sep. 2008

A point whose coordinates satisfy \displaystyle y < 3x-4 has a y-coordinate which is less than that of a point lying on the line \displaystyle y=3x-4 and having the same x-coordinate. This means that the area we should shade consists of all points below the line \displaystyle y=3x-4.



We can draw the line \displaystyle y=3x-4 by choosing two x-values, for example \displaystyle x=0 and \displaystyle x=1, using the equation of the line to calculate the corresponding y-coordinates, \displaystyle y=3\cdot 0-4=-4 and \displaystyle y=3\cdot 1-4=-1 respectively, and then draw a straight line between the two points that we have obtained.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/L%C3%B6sung_2.2:8b“