Lösung 2.2:6b
Aus Online Mathematik Brückenkurs 1
(Unterschied zwischen Versionen)
K |
|||
| Zeile 1: | Zeile 1: | ||
Because the point of intersection lies on both lines, it must satisfy the equations of both lines | Because the point of intersection lies on both lines, it must satisfy the equations of both lines | ||
| + | {{Displayed math||<math>y=-x+5\qquad\text{and}\qquad x=0\,,</math>}} | ||
| - | <math> | + | where <math>x=0</math> is the equation of the ''y''-axis. Substituting the second equation, <math>x=0</math>, into the first equation gives <math>y=-0+5=5</math>. This means that the point of intersection is (0,5). |
| - | + | ||
| - | <math> | + | |
| - | where | ||
| - | <math>x=0</math> | ||
| - | is the equation of the | ||
| - | <math>y</math> | ||
| - | -axis. Substituting the other equation, | ||
| - | <math>x=0</math>, into the first equation gives | ||
| - | <math>y=-0+5=5</math>. This means that the point of intersection is | ||
| - | <math>\left( 0 \right.,\left. 5 \right)</math>. | ||
| - | + | <center>[[Image:2_2_6_b.gif]]</center> | |
| - | + | ||
| - | [[Image:2_2_6_b.gif]] | + | |
| - | + | ||
| - | + | ||
Version vom 13:04, 24. Sep. 2008
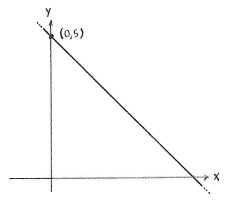
Because the point of intersection lies on both lines, it must satisfy the equations of both lines
where \displaystyle x=0 is the equation of the y-axis. Substituting the second equation, \displaystyle x=0, into the first equation gives \displaystyle y=-0+5=5. This means that the point of intersection is (0,5).