4.1 Winkel und Kreise

Aus Online Mathematik Brückenkurs 1

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Aktuelle Version (13:32, 11. Aug. 2010) (bearbeiten) (rückgängig)
 
(Der Versionsvergleich bezieht 93 dazwischen liegende Versionen mit ein.)
Zeile 2: Zeile 2:
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
| style="border-bottom:1px solid #797979" width="5px" |  
| style="border-bottom:1px solid #797979" width="5px" |  
-
{{Vald flik|[[4.1 Vinklar och cirklar|Theory]]}}
+
{{Gewählter Tab|[[4.1 Winkel und Kreise|Theorie]]}}
-
{{Ej vald flik|[[4.1 Övningar|Exercises]]}}
+
{{Nicht gewählter Tab|[[4.1 Übungen|Übungen]]}}
| style="border-bottom:1px solid #797979" width="100%"|  
| style="border-bottom:1px solid #797979" width="100%"|  
|}
|}
{{Info|
{{Info|
-
'''Contents:'''
+
'''Inhalt:'''
-
*Various angle measures (degrees, radians and revolutions)
+
*Verschiedene Winkelmaße (Grade und Radianten)
-
*The Pythagorean theorem
+
*Der Satz des Pythagoras
-
*Formula for distance in the plane
+
*Die Formel für den Abstand zwischen zwei Punkten
-
* Equation of a circle
+
*Die Gleichung eines Kreises
}}
}}
{{Info|
{{Info|
-
'''Learning outcomes:'''
+
'''Lernziele:'''
-
After this section, you will have learned :
+
Nach diesem Abschnitt solltest Du folgendes können :
-
*To convert between degrees, radians and revolutions.
+
*Winkel von Graden auf Radianten umwandeln.
-
*To calculate the area and circumference of sectors of a circle.
+
*Die Fläche und Länge eines Kreissektors berechnen.
-
*The concepts of right-angled triangles including its legs and hypotenuse.
+
*Die Begriffe Kathete und Hypotenuse kennen.
-
*To formulate and use the Pythagorean theorem.
+
*Das Gesetz des Pythagoras kennen und beherrschen.
-
*To calculate the distance between two points in the plane.
+
*Den Abstand zwischen zwei Punkten berechnen.
-
*To sketch circles by completing the square in their equations.
+
*Kreise zeichnen, die durch eine Gleichung definiert sind.
-
*The concepts of unit circle, tangent, radius, diameter, circumference, chord and arc.
+
*Die Begriffe Einheitskreis, Tangente, Radius, Durchmesser, Umkreis, Sehne und Kreissektor kennen.
-
*To solve geometric problems that contain circles.
+
*Geometrische Probleme mit Kreisen lösen.
}}
}}
-
== Angle measures ==
+
Die Lernziele sind Dir aus der Schule noch bestens vertraut und Du weißt ganz genau, wie man die zugehörigen Rechnungen ausführt? Dann kannst Du auch gleich mit den <b>Prüfungen</b> beginnen (Du findest den Link in der Student Lounge).
-
There are several different units for measuring angles, which are used in different contexts. The two most common within mathematics are degrees and radians.
+
== A - Winkeleinheiten ==
-
*'''Degrees.''' If a complete revolution is divided into 360 parts, then each part is called 1 degree. Degrees are designated by <math>{}^\circ</math>.
+
Es gibt viele verschiedene Winkeleinheiten, die in verschiedenen Bereichen verwendet werden. Die zwei häufigsten sind Grad und Radiant.
-
[[Bild:Gradskiva - 57°.gif||center]]
+
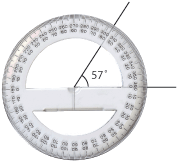
*'''Grad.''' Wenn man einen Kreis in 360 gleich große Stücke aufteilt, wird jedes Teil ein Grad genannt. Man bezeichnet die Einheit Grad mit <math>{}^\circ</math>.
-
*'''Radians.''' Another way to measure an angle, is to use the length of the arc which subtends the angle in relation to the radius as a measure of the angle. This unit is called radian. A revolution is <math>2\pi</math> radians as the circumference of a circle is <math>2\pi r</math>, where <math>r</math> is the radius of the circle.
+
[[Image:Gradskiva - 57°.gif||center]]
-
[[Bild:Gradskiva - Radianer.gif||center]]
+
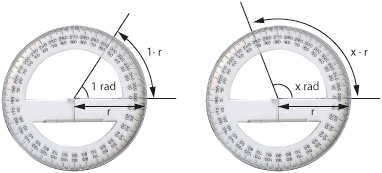
*'''Radiant.''' Eine andere Winkeleinheit ist der Radiant. Der Radiant wird oft ''rad'' geschrieben. Ein Radiant wird definiert dadurch, dass ein Kreis den Winkel <math>2\pi</math> rad hat.
 +
[[Image:Gradskiva - Radianer.gif||center]]
-
A complete revolution is <math>360^\circ</math> or <math>2\pi</math> radians which means
+
 
-
{{Fristående formel||<math>\begin{align*}
+
Ein Vollwinkel besteht aus <math>360^\circ</math> oder <math>2\pi</math> rad, also ist
-
&1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radians }
+
{{Abgesetzte Formel||<math>\begin{align*}
-
= \frac{\pi}{180}\ \mbox{ radians,}\\
+
&1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radians }
-
&1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ
+
= \frac{\pi}{180}\ \mbox{ radians,}\\
-
= \frac{180^\circ}{\pi}\,\mbox{.}
+
&1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ
-
\end{align*}</math>}}
+
= \frac{180^\circ}{\pi}\,\mbox{.}
-
These conversion relations can be used to convert between degrees and radians.
+
\end{align*}</math>}}
 +
Mit diesem Verhältnis kann man Winkel von den Einheiten Grad in Radiant umwandeln.
<div class="exempel">
<div class="exempel">
-
''' Example 1'''
+
''' Beispiel 1'''
<ol type="a">
<ol type="a">
<li><math>30^\circ = 30 \cdot 1^\circ
<li><math>30^\circ = 30 \cdot 1^\circ
-
= 30 \cdot \frac{\pi}{180}\ \mbox{ radians }
+
= 30 \cdot \frac{\pi}{180}\ \mbox{ rad }
-
= \frac{\pi}{6}\ \mbox{ radians }</math></li>
+
= \frac{\pi}{6}\ \mbox{ rad }</math></li>
<li><math>\frac{\pi}{8}\ \mbox { radians }
<li><math>\frac{\pi}{8}\ \mbox { radians }
-
= \frac{\pi}{8} \cdot (1 \; \mbox{radians}\,)
+
= \frac{\pi}{8} \cdot (1 \; \mbox{rad}\,)
= \frac{\pi}{8} \cdot \frac{180^\circ}{\pi}
= \frac{\pi}{8} \cdot \frac{180^\circ}{\pi}
= 22{,}5^\circ</math></li>
= 22{,}5^\circ</math></li>
Zeile 66: Zeile 68:
</div>
</div>
-
In some contexts, it may be useful to talk about negative angles and angles greater than 360°. This means that the same direction can be designated by different angles that differ from each other by an integral number of revolutions.
+
Manchmal spricht man von Winkeln, die negativ oder größer als <math>360 \, ^{\circ}</math> sind. Dies bedeutet, dass ein Punkt am Kreis durch mehrere Winkel repräsentiert werden kann.
-
<center>{{:4.1 - Figur - Vinklarna 45°, -315° och 405°}}</center>
+
<center>{{:4.1 - Bild - Die Winkeln 45°, -315° und 405°}}</center>
<div class="exempel">
<div class="exempel">
-
''' Example 2'''
+
''' Beispiel 2'''
<ol type="a">
<ol type="a">
-
<li> The angles <math>-55^\circ</math> and <math>665^\circ
+
<li> Die Winkel <math>-55^\circ</math> und <math>665^\circ
-
</math> indicate the same direction because
+
</math> repräsentieren denselben Punkt, weil
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
-55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}</math>}}</li>
+
-55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}</math>}}</li>
-
<li> The angles <math>\frac{3\pi}{7}</math> and <math>
+
<li> Die Winkel <math>\frac{3\pi}{7}</math> und <math>
-
-\frac{11\pi}{7}</math> indicate the same direction because
+
-\frac{11\pi}{7}</math> repräsentieren denselben Punkt, weil
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
\frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}</math>}}</li>
+
\frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}</math>}}</li>
-
<li> The angles <math>36^\circ</math> and <math>
+
<li> Die Winkel <math>36^\circ</math> und <math>
-
216^\circ</math> do not specify the same direction, but opposite directions since
+
216^\circ</math> repräsentieren nicht denselben Punkt, weil
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
36^\circ + 180^\circ = 216^\circ\,\mbox{.}</math>}}</li>
+
36^\circ + 180^\circ = 216^\circ\,\mbox{.}</math>}}</li>
</ol>
</ol>
</div>
</div>
 +
Neben dem Vollwinkel sind noch folgende Ausdrücke von Bedeutung:
 +
* Spitzer Winkel: Ein Winkel, der kleiner ist als <math> \frac{1}{4} </math> des Vollwinkels. Also für einen Winkel x: <math> 0 < x < 90^\circ \text{ bzw. } \frac{\pi}{2} </math>
 +
* Rechter Winkel: Ein Winkel von genau <math> 90^\circ \text{ bzw. } \frac{\pi}{2} </math>.
 +
* Stumpfer Winkel: Ein Winkel, der größer als <math> \frac{1}{4} </math> aber kleiner als <math> \frac{1}{2} </math> des Vollwinkels ist. Also für einen Winkel x: <math> 90^\circ \text{ bzw. } \frac{\pi}{2} < x < 180^\circ \text{ bzw. } \pi </math>
-
== Formula for distance in the plane ==
+
== B - Abstand zwischen zwei Punkten ==
-
The theorem of Pythagoras is one of the most famous theorems in mathematics and says that in a right-angled triangle with the legs <math>a</math> and <math>b</math>, and the hypotenuse <math>c</math> then
+
Der Satz des Pythagoras ist einer der berühmtesten Sätze der Mathematik. Der Satz des Pythagoras sagt: wenn <math>a</math> und <math>b</math> die Katheten eines rechtwinkligen Dreiecks sind und <math>c</math> die Hypotenuse, dann gilt:
<div class="regel">
<div class="regel">
{|width="100%"
{|width="100%"
-
|width="100%"|'''The Pythagorean theorem:'''
+
|width="100%"|'''Satz des Pythagoras:'''
-
{{Fristående formel||<math>c^2 = a^2 + b^2\,\mbox{.}</math>}}
+
{{Abgesetzte Formel||<math>c^2 = a^2 + b^2\,\mbox{.}</math>}}
-
|align="right"|{{:4.1 - Figur - Pythagoras sats}}
+
|align="right"|{{:4.1 - Bild - Satz des Pythagoras}}
|}
|}
</div>
</div>
<div class="exempel">
<div class="exempel">
-
''' Example 3'''
+
''' Beispiel 3'''
{| width="100%"
{| width="100%"
-
|width="100%"| The triangle on the right is
+
|width="100%"| Wir erhalten c durch den Satz des Pythagoras:
-
{{Fristående formel||<math>c^2= 3^2 + 4^2 = 9 +16 = 25</math>}}
+
{{Abgesetzte Formel||<math>c^2= 3^2 + 4^2 = 9 +16 = 25</math>}}
-
and therefore hypotenuse <math>c</math> is equal to
+
und daher ist
-
{{Fristående formel||<math>c=\sqrt{25} = 5\,\mbox{.}</math>}}
+
{{Abgesetzte Formel||<math>c=\sqrt{25} = 5\,\mbox{.}</math>}}
-
|align="right"|{{:4.1 - Figur - Rätvinklig triangel med sidor 3, 4 och 5}}
+
|align="right"|{{:4.1 - Bild - Ein rechteckiges Dreieck mit den Seiten 3, 4 und 5}}
|}
|}
</div>
</div>
-
The Pythagorean theorem can be used to calculate the distance between two points in a coordinate system.
+
Der Satz des Pythagoras kann verwendet werden, um den Abstand zwischen zwei Punkten zu bestimmen.
<div class="regel">
<div class="regel">
-
'''Formula for distance:'''
+
'''Abstand zwischen zwei Punkten:'''
-
The distance <math>d</math> between two points with coordinates <math>(x,y)</math> and <math>(a,b)</math> is
+
Der Abstand <math>d</math> zwischen den Punkten <math>(x,y)</math> und <math>(a,b)</math> ist
-
{{Fristående formel||<math>d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}</math>}}
+
{{Abgesetzte Formel||<math>d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}</math>}}
</div>
</div>
-
The line joining the points is the hypotenuse of a triangle whose legs are parallel to the coordinate axes.
+
Die Gerade zwischen den beiden Punkten ist die Hypotenuse eines Dreiecks, wobei die Katheten parallel zu den Koordinatenachsen sind.
-
<center>{{:4.1 - Figur - Avståndsformeln}}</center>
+
<center>{{:4.1 - Bild - Die Abstandsformel}}</center>
-
The legs of the triangle have lengths equal to the difference in the ''x''- and ''y''-directions of the points, that is <math>|x-a|</math> and <math>|y-b|</math>. The Pythagorean theorem then gives the formula for the distance.
+
Die Katheten des Dreiecks sind die Unterschiede in ''x''- bzw. in ''y''-Richtung der Punkte, also <math>|x-a|</math> und <math>|y-b|</math>. Durch den Satz des Pythagoras erhalten wir den Abstand zwischen den Punkten.
<div class="exempel">
<div class="exempel">
-
''' Example 4'''
+
''' Beispiel 4'''
<ol type="a">
<ol type="a">
-
<li>The distance between <math>(1,2)</math> and <math>(3,1)</math> is
+
<li>Der Abstand zwischen <math>(1,2)</math> und <math>(3,1)</math> ist
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
d = \sqrt{ (1-3)^2 + (2-1)^2}
+
d = \sqrt{ (1-3)^2 + (2-1)^2}
-
= \sqrt{(-2)^2 + 1^2}
+
= \sqrt{(-2)^2 + 1^2}
-
= \sqrt{ 4+1}
+
= \sqrt{ 4+1}
-
= \sqrt{5}\,\mbox{.}</math>}}</li>
+
= \sqrt{5}\,\mbox{.}</math>}}</li>
-
<li>The distance between <math>(-1,0)</math> and <math>(-2,-5)</math> is
+
<li>Der Abstand zwischen <math>(-1,0)</math> und <math>(-2,-5)</math> ist
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2}
+
d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2}
-
= \sqrt{1^2 + 5^2}
+
= \sqrt{1^2 + 5^2}
-
= \sqrt{1+25}
+
= \sqrt{1+25}
-
= \sqrt{26}\,\mbox{.}</math>}}</li>
+
= \sqrt{26}\,\mbox{.}</math>}}</li>
</ol>
</ol>
</div>
</div>
-
== Circles ==
+
== C - Kreise ==
-
A circle consists of all the points that are at a given fixed distance <math>r</math> from a point <math>(a,b)</math>.
+
Ein Kreis besteht aus allen Punkten, die auf dem Abstand <math>r</math> von einem bestimmten Punkt <math>(a,b)</math> liegen.
-
<center>{{:4.1 - Figur - Cirkel}}</center>
+
<center>{{:4.1 - Bild - Kreis}}</center>
-
 
+
Der Abstand <math>r</math> ist der Radius des Kreises und der Punkt <math>(a,b)</math> dessen Mittelpunkt. Das Bild zeigt andere wichtige Begriffe eines Kreises.
-
The distance <math>r</math> is called the circle´s radius and the point <math>(a,b)</math> is its centre. The figure below shows the other important concepts.
+
{| align="center"
{| align="center"
-
|align="center" valign="bottom"|{{:4.1 - Figur - Diameter}}
+
|align="center" valign="bottom"|{{:4.1 - Bild - Diameter}}
|width="15px"|
|width="15px"|
-
|align="center" valign="bottom"|{{:4.1 - Figur - Tangent}}
+
|align="center" valign="bottom"|{{:4.1 - Bild - Tangente}}
|width="15px"|
|width="15px"|
-
|align="center" valign="bottom"|{{:4.1 - Figur - Korda}}
+
|align="center" valign="bottom"|{{:4.1 - Bild - Chordale eines Kreises}}
|width="15px"|
|width="15px"|
-
|align="center" valign="bottom"|{{:4.1 - Figur - Sekant}}
+
|align="center" valign="bottom"|{{:4.1 - Bild - Sekante}}
|-
|-
-
|align="center"|Diameter
+
|align="center"|Durchmesser
||
||
-
|align="center"|Tangent
+
|align="center"|Tangente
||
||
-
|align="center"| Chord
+
|align="center"|Sehne
||
||
-
|align="center"| Secant
+
|align="center"|Sekante
-
|-
+
-
|height="15px"|
+
|-
|-
-
|align="center"|{{:4.1 - Figur - Cirkelbåge}}
+
|align="center"|{{:4.1 - Bild - Kreisbogen}}
||
||
-
|align="center"|{{:4.1 - Figur - Periferi}}
+
|align="center"|{{:4.1 - Bild - Umfang}}
||
||
-
|align="center"|{{:4.1 - Figur - Cirkelsektor}}
+
|align="center"|{{:4.1 - Bild - Kreissektor}}
||
||
-
|align="center"|{{:4.1 - Figur - Cirkelsegment}}
+
|align="center"|{{:4.1 - Bild - Kreissegment}}
|-
|-
-
|align="center"| Arc of a circle
+
|align="center"|Kreisbogen
||
||
-
|align="center"| circumference
+
|align="center"|Umfang
||
||
-
|align="center"| sector of a circle
+
|align="center"|Sektor eines Kreises
||
||
-
|align="center"|segment of a circle
+
|align="center"|Segment eines Kreises
|}
|}
 +
 +
 +
Nützliche Formeln zur Berechnung des Kreisumfanges und der Kreisfläche.
 +
<div class="regel">
 +
{{Abgesetzte Formel|| Kreisumfang <math> = 2 \pi r </math>
 +
Kreisfläche <math> = \pi r^2 </math> }}
 +
</div>
 +
<div class="exempel">
<div class="exempel">
-
''' Example 5'''
+
''' Beispiel 5'''
{| width="100%"
{| width="100%"
-
||A sector of a circle is given in the figure on the right.
+
||Ein Kreisbogen ist in der Figur eingezeichnet.
<ol type="a">
<ol type="a">
-
<li> Determine its arc length .
+
<li> Bestimme die Länge des Kreisbogens
<br>
<br>
<br>
<br>
-
The central angle <math>50^\circ</math> is in radians
+
Der Winkel <math>50^\circ</math> ist in Radianten
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
50^\circ = 50 \cdot 1^\circ
+
50^\circ = 50 \cdot 1^\circ
-
= 50 \cdot \frac{\pi}{180}\ \mbox{ radians }
+
= 50 \cdot \frac{\pi}{180}\ \mbox{ rad }
-
= \frac{5\pi}{18}\ \mbox{ radians. }</math>}}
+
= \frac{5\pi}{18}\ \mbox{ rad. }</math>}}
</li>
</li>
</ol>
</ol>
|align="right" valign="top"|
|align="right" valign="top"|
-
{{:4.1 - Figur - Cirkelsektor 50°}}
+
{{:4.1 - Bild - 50° Kreissektor}}
|}
|}
<ol style="list-style-type:none; padding-top:0; margin-top:0;">
<ol style="list-style-type:none; padding-top:0; margin-top:0;">
-
<li>The way radians have been defined means that the arc length is the radius multiplied by the angle measured in radians,
+
<li>Laut Definition des Radianten ist die Länge des Kreisbogens der Winkel in Radianten multipliziert mit dem Radius
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
3 \cdot \frac{5\pi}{18}\ \mbox{units }
+
3 \cdot \frac{5\pi}{18}\ \mbox{ Einheiten }
-
= \frac{5\pi}{6}\ \mbox{ units . }</math>}}</li>
+
= \frac{5\pi}{6}\ \mbox{ Einheiten . }</math>}}</li>
</ol>
</ol>
<ol type="a" start="2">
<ol type="a" start="2">
-
<li>Determine the area of the circle segment.
+
<li>Bestimmen sie die Fläche des Kreissektors
<br>
<br>
<br>
<br>
-
The circle segment´s share of the entire circle is
+
Der Kreissektor nimmt den Anteil
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
\frac{50^\circ}{360^\circ} = \frac{5}{36}</math>}}
+
\frac{50^\circ}{360^\circ} = \frac{5}{36}</math>}}
-
and this means that its area is <math>\frac{5}{36}</math> parts of the circle area, which is <math>\pi r^2 = \pi 3^2 = 9\pi</math>, i.e.
+
der Fläche des Kreises ein. Deshalb ist die Fläche des Kreissektors <math>\frac{5}{36}</math> von der ganzen Fläche des Kreises, welche <math>\pi r^2 = \pi 3^2 = 9\pi</math> ist. Also ist die Fläche des Kreissektors
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
\frac{5}{36} \cdot 9\pi\ \mbox{ units }= \frac{5\pi}{4}\ \mbox{ units. }</math>}}</li>
+
\frac{5}{36} \cdot 9\pi\ \mbox{ Einheiten }= \frac{5\pi}{4}\ \mbox{ Einheiten. }</math>}}</li>
</ol>
</ol>
</div>
</div>
-
A point <math>(x,y)</math> lies on the circle that has its centre at <math>(a,b)</math> and radius <math>r</math>, if its distance from the centre is equal to <math>r</math>. This condition can be formulated with the distance formula as
+
Die Punkte <math>(x,y)</math>, die auf dem Kreis mit dem Mittelpunkt <math>(a,b)</math> und dem Radius <math>r</math> liegen, können durch die Formel für den Abstand zwischen zwei Punkten beschrieben werden.
<div class="regel">
<div class="regel">
{| width="100%"
{| width="100%"
-
||'''Circle equation: '''
+
||'''Die Gleichung eines Kreises: '''
-
{{Fristående formel||<math>(x – a)^2 + (y – b)^2 = r^2\,\mbox{.}</math>}}
+
{{Abgesetzte Formel||<math>(x – a)^2 + (y – b)^2 = r^2\,\mbox{.}</math>}}
-
|align="right"|{{:4.1 - Figur - Cirkelns ekvation}}
+
|align="right"|{{:4.1 - Bild - Gleichung eines Kreises}}
|}
|}
</div>
</div>
<div class="exempel">
<div class="exempel">
-
''' Example 6'''
+
''' Beispiel 6'''
{| width="100%"
{| width="100%"
|-
|-
|width="100%"|
|width="100%"|
<ol type="a">
<ol type="a">
-
<li><math>(x-1)^2 + (y-2)^2 = 9\quad</math> is the equation for a circle with its centre at <math>(1,2)</math> and radius <math>\sqrt{9} = 3</math>.</li>
+
<li><math>(x-1)^2 + (y-2)^2 = 9\quad</math> ist die Gleichung eines Kreises mit dem Mittelpunkt <math>(1,2)</math> und dem Radius <math>\sqrt{9} = 3</math>.</li>
</ol>
</ol>
-
|align="right"|{{:4.1 - Figur - Ekvationen (x - 1)² + (y - 2)² = 9}}
+
|align="right"|{{:4.1 - Bild - Die Gleichung (x - 1)² + (y - 2)² = 9}}
|-
|-
|width="100%"|
|width="100%"|
<ol type="a" start=2>
<ol type="a" start=2>
-
<li><math>x^2 + (y-1)^2 = 1\quad</math> can be written as <math>(x-0)^2 + (y-1)^2 = 1</math> and is the equation of a circle with its centre at <math>(0,1)</math> and having a radius <math>\sqrt{1} = 1</math>.</li>
+
<li><math>x^2 + (y-1)^2 = 1\quad</math>: Es gilt <math>(x-0)^2 + (y-1)^2 = 1</math>, also ist dies die Gleichung eines Kreises mit dem Mittelpunkt <math>(0,1)</math> und dem Radius <math>\sqrt{1} = 1</math>.</li>
</ol>
</ol>
-
|align="right"|{{:4.1 - Figur - Ekvationen x² + (y - 1)² = 1}}
+
|align="right"|{{:4.1 - Bild - Die Gleichung x² + (y - 1)² = 1}}
|-
|-
|width="100%"|
|width="100%"|
<ol type="a" start=3>
<ol type="a" start=3>
-
<li><math>(x+1)^2 + (y-3)^2 = 5\quad</math> can be written as <math>(x-(-1))^2 + (y-3)^2 = 5</math> and is the equation of a circle with its centre at <math>(-1,3)</math> and having a radius <math>\sqrt{5} \approx 2\textrm{.}236</math>.</li>
+
<li><math>(x+1)^2 + (y-3)^2 = 5\quad</math>: es ist <math>(x-(-1))^2 + (y-3)^2 = 5</math>, also ist dies Gleichung eines Kreises mit dem Mittelpunkt <math>(-1,3)</math> und dem Radius <math>\sqrt{5} \approx 2\textrm{.}236</math>.</li>
</ol>
</ol>
-
|align="right"|{{:4.1 - Figur - Ekvationen (x + 1)² + (y - 3)² = 5}}
+
|align="right"|{{:4.1 - Bild - Die Gleichung (x + 1)² + (y - 3)² = 5}}
|}
|}
</div>
</div>
<div class="exempel">
<div class="exempel">
-
''' Example 7'''
+
''' Beispiel 7'''
<ol type="a">
<ol type="a">
-
<li> Does the point <math>(1,2)</math> lie on the circle <math>(x-4)^2 +y^2=13</math>?
+
<li> Liegt der Punkt <math>(1,2)</math> auf dem Kreis <math>(x-4)^2 +y^2=13</math>?
<br>
<br>
<br>
<br>
-
Inserting the coordinates of the point <math>x=1</math> and <math>y=2</math> in the circle equation, we have that
+
Wir kontrollieren, ob <math>x=1</math> und <math>y=2</math> die Gleichung des Kreises erfüllen:
-
{{Fristående formel||<math>\begin{align*}
+
{{Abgesetzte Formel||<math>\begin{align*}
-
\mbox{LHS } &= (1-4)^2+2^2\\
+
\mbox{linke Seite } &= (1-4)^2+2^2\\
-
&= (-3)^2+2^2 = 9+4 = 13 = \mbox{RHS}\,\mbox{.}
+
&= (-3)^2+2^2 = 9+4 = 13 = \mbox{Rechte Seite}\,\mbox{.}
-
\end{align*}</math>}}
+
\end{align*}</math>}}
-
Since the point satisfies the circle equation it lies on the circle.
+
Nachdem der Punkt die Gleichung des Kreises erfüllt, liegt er auf dem Kreis.
-
<center>{{:4.1 - Figur - Ekvationen (x - 4)² + y² = 13}}</center></li>
+
<center>{{:4.1 - Bild - Die Gleichung (x - 4)² + y² = 13}}</center></li>
-
<li> Determine the equation for the circle that has its centre at <math>(3,4)</math> and goes through the point <math>(1,0)</math>.
+
<li> Bestimmen Sie die Gleichung für den Kreis, der den Mittelpunkt <math>(3,4)</math> hat und durch den Punkt <math>(1,0)</math> geht.
<br>
<br>
<br>
<br>
-
Since the point <math>(1,0)</math> lies on the circle, the radius of the circle must be equal to the distance of the point from <math>(1,0)</math> to the centre <math>(3,4)</math>. The distance formula gives that this distance is
+
Nachdem der Punkt <math>(1,0)</math> auf dem Kreis liegt, muss der Abstand zwischen diesem Punkt und dem Mittelpunkt <math>(3,4)</math> der Radius des Kreises sein. Also haben wir
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{.}</math>}}
+
c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{}</math>}}
-
The circle equation is therefore
+
und die Gleichung des Kreises lautet:
-
{{Fristående formel||<math>(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}</math>}}
+
{{Abgesetzte Formel||<math>(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}</math>}}
-
<center>{{:4.1 - Figur - Ekvationen (x - 3)² + (y - 4)² = 20}}</center></li>
+
<center>{{:4.1 - Bild - Die Gleichung (x - 3)² + (y - 4)² = 20}}</center></li>
</ol>
</ol>
</div>
</div>
Zeile 296: Zeile 307:
<div class="exempel">
<div class="exempel">
-
''' Example 8'''
+
''' Beispiel 8'''
-
Determine the centre and radius of the circle with equation <math>\ x^2 + y^2 – 2x + 4y + 1 = 0</math>.
+
Bestimme den Mittelpunkt und Radius des Kreises mit der Gleichung <math>\ x^2 + y^2 – 2x + 4y + 1 = 0</math>.
-
Let us try to write the equation of the circle in the form
+
Wir wollen die Gleichung des Kreises auf die Form
-
{{Fristående formel||<math>(x – a)^2 + (y – b)^2 = r^2</math>}}
+
{{Abgesetzte Formel||<math>(x – a)^2 + (y – b)^2 = r^2</math>}}
-
because then we can directly read from this that the midpoint is <math>(a,b)</math> and the radius is <math>r</math>.
+
bringen. Dann können wir den Mittelpunkt direkt als <math>(a,b)</math> ablesen, und den Radius als <math>r</math>.
-
Start by completing the square for the terms containing <math>x</math> on the left-hand side
+
Wir benutzen zuerst die quadratische Ergänzung für alle <math>x</math>-Terme auf der linken Seite
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
\underline{x^2-2x\vphantom{(}} + y^2+4y + 1
+
\underline{x^2-2x\vphantom{(}} + y^2+4y + 1
-
= \underline{(x-1)^2-1^2} + y^2+4y + 1</math>}}
+
= \underline{(x-1)^2-1^2} + y^2+4y + 1</math>}}
-
(the underlined terms shows the terms involved).
+
(Wir haben nur die unterstrichenen Terme verändert)
-
Complete the square for the terms containing <math>y</math>
+
Jetzt benutzen wir die quadratische Ergänzung für alle <math>y</math>-Terme
-
{{Fristående formel||<math>
+
{{Abgesetzte Formel||<math>
-
(x-1)^2-1^2 + \underline{y^2+4y} + 1
+
(x-1)^2-1^2 + \underline{y^2+4y} + 1
-
= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}</math>}}
+
= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}</math>}}
 +
Die linke Seite ist also
 +
{{Abgesetzte Formel||<math> (x-1)^2 + (y+2)^2-4 </math>}}
-
The left-hand side is equal to
+
Wenn wir 4 zu beiden Seiten addieren, erhalten wir
-
{{Fristående formel||<math> (x-1)^2 + (y+2)^2-4 </math>}}
+
{{Abgesetzte Formel||<math> (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}</math>}}
-
and moving over the 4 to to the right-hand side we get the equation
+
Also hat der Kreis den Mittelpunkt <math>(1,-2)</math> und den Radius <math>\sqrt{4}= 2</math>.
-
{{Fristående formel||<math> (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}</math>}}
+
-
We can interpret this as follows: The centre is at <math>(1,-2)</math> and the radius is <math>\sqrt{4}= 2</math>.
+
<center>{{:4.1 - Bild - Die Gleichung x² + y² - 2x + 4y + 1 = 0}}</center>
-
 
+
-
<center>{{:4.1 - Figur - Ekvationen x² + y² - 2x + 4y + 1 = 0}}</center>
+
</div>
</div>
 +
<br><br>
 +
 +
Noch Fragen zu diesem Kapitel? Dann schau nach im Kursforum (Du findest den Link in der Student Lounge) oder frag nach per Skype bei ombTutor <skype style="call" action="call">ombTutor</skype> <skype style="chat" action="chat">ombTutor</skype>
 +
Keine Fragen mehr? Dann mache weiter mit den '''[[4.1 Übungen|Übungen]]''' .
-
[[4.1 Övningar|Exercises]]
 
<div class="inforuta" style="width:580px;">
<div class="inforuta" style="width:580px;">
-
'''Study advice'''
+
'''Tipps fürs Lernen'''
-
'''The basic and final tests'''
+
'''Diagnostische Prüfung und Schlussprüfung'''
-
After you have read the text and worked through the exercises, you should do the basic and final tests to pass this section. You can find the link to the tests in your student lounge.
+
Nachdem du mit der Theorie und den Übungen fertig bist, solltest Du die diagnostische Prüfung und die Schlussprüfung machen. Du findest die Links zu den Prüfungen in Deiner "Student Lounge".
 +
'''Bedenken Sie folgendes:'''
-
'''Keep in mind that:'''
 
 +
'''Literaturhinweise'''
-
'''Reviews'''
+
Für die, die tiefer in die Materie einsteigen wollen, sind hier einige Links angeführt:
-
For those of you who want to deepen your studies or need more detailed explanations consider the following references:
 
-
[http://sv.wikipedia.org/wiki/Pythagoras_sats Learn more about Pythagoras theorem in English Wikipedia ]
+
[http://de.wikipedia.org/wiki/Satz_des_Pythagoras Mehr über den Satz des Pythagoras in der Wikipedia ]
-
[http://mathworld.wolfram.com/Circle.html Read more in Mathworld about the circle ]
+
[http://mathworld.wolfram.com/Circle.html Lies mehr über Kreise auf Mathworld (engl.)]
-
'''Useful web sites'''
+
'''Nützliche Websites'''
-
[http://www.math.kth.se/online/images/sinus_och_cosinus_i_enhetscirkeln.swf Interactive experiments: the sine and cosine on the unit circle ] (Flash)
+
[http://www.math.kth.se/online/images/sinus_och_cosinus_i_enhetscirkeln.swf Interaktive Experimente: Sinus und Cosinus im Einheitskreis ] (Flash)
</div>
</div>

Aktuelle Version

       Theorie          Übungen      

Inhalt:

  • Verschiedene Winkelmaße (Grade und Radianten)
  • Der Satz des Pythagoras
  • Die Formel für den Abstand zwischen zwei Punkten
  • Die Gleichung eines Kreises

Lernziele:

Nach diesem Abschnitt solltest Du folgendes können :

  • Winkel von Graden auf Radianten umwandeln.
  • Die Fläche und Länge eines Kreissektors berechnen.
  • Die Begriffe Kathete und Hypotenuse kennen.
  • Das Gesetz des Pythagoras kennen und beherrschen.
  • Den Abstand zwischen zwei Punkten berechnen.
  • Kreise zeichnen, die durch eine Gleichung definiert sind.
  • Die Begriffe Einheitskreis, Tangente, Radius, Durchmesser, Umkreis, Sehne und Kreissektor kennen.
  • Geometrische Probleme mit Kreisen lösen.

Die Lernziele sind Dir aus der Schule noch bestens vertraut und Du weißt ganz genau, wie man die zugehörigen Rechnungen ausführt? Dann kannst Du auch gleich mit den Prüfungen beginnen (Du findest den Link in der Student Lounge).

A - Winkeleinheiten

Es gibt viele verschiedene Winkeleinheiten, die in verschiedenen Bereichen verwendet werden. Die zwei häufigsten sind Grad und Radiant.

  • Grad. Wenn man einen Kreis in 360 gleich große Stücke aufteilt, wird jedes Teil ein Grad genannt. Man bezeichnet die Einheit Grad mit \displaystyle {}^\circ.
  • Radiant. Eine andere Winkeleinheit ist der Radiant. Der Radiant wird oft rad geschrieben. Ein Radiant wird definiert dadurch, dass ein Kreis den Winkel \displaystyle 2\pi rad hat.


Ein Vollwinkel besteht aus \displaystyle 360^\circ oder \displaystyle 2\pi rad, also ist

\displaystyle \begin{align*}

&1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radians } = \frac{\pi}{180}\ \mbox{ radians,}\\ &1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ = \frac{180^\circ}{\pi}\,\mbox{.} \end{align*}

Mit diesem Verhältnis kann man Winkel von den Einheiten Grad in Radiant umwandeln.

Beispiel 1

  1. \displaystyle 30^\circ = 30 \cdot 1^\circ = 30 \cdot \frac{\pi}{180}\ \mbox{ rad } = \frac{\pi}{6}\ \mbox{ rad }
  2. \displaystyle \frac{\pi}{8}\ \mbox { radians } = \frac{\pi}{8} \cdot (1 \; \mbox{rad}\,) = \frac{\pi}{8} \cdot \frac{180^\circ}{\pi} = 22{,}5^\circ

Manchmal spricht man von Winkeln, die negativ oder größer als \displaystyle 360 \, ^{\circ} sind. Dies bedeutet, dass ein Punkt am Kreis durch mehrere Winkel repräsentiert werden kann.

[Image]

Beispiel 2

  1. Die Winkel \displaystyle -55^\circ und \displaystyle 665^\circ repräsentieren denselben Punkt, weil
    \displaystyle

    -55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}

  2. Die Winkel \displaystyle \frac{3\pi}{7} und \displaystyle -\frac{11\pi}{7} repräsentieren denselben Punkt, weil
    \displaystyle

    \frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}

  3. Die Winkel \displaystyle 36^\circ und \displaystyle 216^\circ repräsentieren nicht denselben Punkt, weil
    \displaystyle

    36^\circ + 180^\circ = 216^\circ\,\mbox{.}

Neben dem Vollwinkel sind noch folgende Ausdrücke von Bedeutung:

  • Spitzer Winkel: Ein Winkel, der kleiner ist als \displaystyle \frac{1}{4} des Vollwinkels. Also für einen Winkel x: \displaystyle 0 < x < 90^\circ \text{ bzw. } \frac{\pi}{2}
  • Rechter Winkel: Ein Winkel von genau \displaystyle 90^\circ \text{ bzw. } \frac{\pi}{2} .
  • Stumpfer Winkel: Ein Winkel, der größer als \displaystyle \frac{1}{4} aber kleiner als \displaystyle \frac{1}{2} des Vollwinkels ist. Also für einen Winkel x: \displaystyle 90^\circ \text{ bzw. } \frac{\pi}{2} < x < 180^\circ \text{ bzw. } \pi

B - Abstand zwischen zwei Punkten

Der Satz des Pythagoras ist einer der berühmtesten Sätze der Mathematik. Der Satz des Pythagoras sagt: wenn \displaystyle a und \displaystyle b die Katheten eines rechtwinkligen Dreiecks sind und \displaystyle c die Hypotenuse, dann gilt:

Satz des Pythagoras:
\displaystyle c^2 = a^2 + b^2\,\mbox{.}

[Image]

Beispiel 3

Wir erhalten c durch den Satz des Pythagoras:
\displaystyle c^2= 3^2 + 4^2 = 9 +16 = 25

und daher ist

\displaystyle c=\sqrt{25} = 5\,\mbox{.}

[Image]

Der Satz des Pythagoras kann verwendet werden, um den Abstand zwischen zwei Punkten zu bestimmen.

Abstand zwischen zwei Punkten:

Der Abstand \displaystyle d zwischen den Punkten \displaystyle (x,y) und \displaystyle (a,b) ist

\displaystyle d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}

Die Gerade zwischen den beiden Punkten ist die Hypotenuse eines Dreiecks, wobei die Katheten parallel zu den Koordinatenachsen sind.

[Image]

Die Katheten des Dreiecks sind die Unterschiede in x- bzw. in y-Richtung der Punkte, also \displaystyle |x-a| und \displaystyle |y-b|. Durch den Satz des Pythagoras erhalten wir den Abstand zwischen den Punkten.

Beispiel 4

  1. Der Abstand zwischen \displaystyle (1,2) und \displaystyle (3,1) ist
    \displaystyle

    d = \sqrt{ (1-3)^2 + (2-1)^2} = \sqrt{(-2)^2 + 1^2} = \sqrt{ 4+1} = \sqrt{5}\,\mbox{.}

  2. Der Abstand zwischen \displaystyle (-1,0) und \displaystyle (-2,-5) ist
    \displaystyle

    d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2} = \sqrt{1^2 + 5^2} = \sqrt{1+25} = \sqrt{26}\,\mbox{.}


C - Kreise

Ein Kreis besteht aus allen Punkten, die auf dem Abstand \displaystyle r von einem bestimmten Punkt \displaystyle (a,b) liegen.

[Image]

Der Abstand \displaystyle r ist der Radius des Kreises und der Punkt \displaystyle (a,b) dessen Mittelpunkt. Das Bild zeigt andere wichtige Begriffe eines Kreises.

[Image]

[Image]

[Image]

[Image]

Durchmesser Tangente Sehne Sekante

[Image]

[Image]

[Image]

[Image]

Kreisbogen Umfang Sektor eines Kreises Segment eines Kreises


Nützliche Formeln zur Berechnung des Kreisumfanges und der Kreisfläche.

Kreisumfang \displaystyle = 2 \pi r

Kreisfläche \displaystyle = \pi r^2


Beispiel 5

Ein Kreisbogen ist in der Figur eingezeichnet.
  1. Bestimme die Länge des Kreisbogens

    Der Winkel \displaystyle 50^\circ ist in Radianten
    \displaystyle

    50^\circ = 50 \cdot 1^\circ = 50 \cdot \frac{\pi}{180}\ \mbox{ rad } = \frac{5\pi}{18}\ \mbox{ rad. }

[Image]

  1. Laut Definition des Radianten ist die Länge des Kreisbogens der Winkel in Radianten multipliziert mit dem Radius
    \displaystyle

    3 \cdot \frac{5\pi}{18}\ \mbox{ Einheiten } = \frac{5\pi}{6}\ \mbox{ Einheiten . }

  1. Bestimmen sie die Fläche des Kreissektors

    Der Kreissektor nimmt den Anteil
    \displaystyle

    \frac{50^\circ}{360^\circ} = \frac{5}{36}

    der Fläche des Kreises ein. Deshalb ist die Fläche des Kreissektors \displaystyle \frac{5}{36} von der ganzen Fläche des Kreises, welche \displaystyle \pi r^2 = \pi 3^2 = 9\pi ist. Also ist die Fläche des Kreissektors

    \displaystyle

    \frac{5}{36} \cdot 9\pi\ \mbox{ Einheiten }= \frac{5\pi}{4}\ \mbox{ Einheiten. }

Die Punkte \displaystyle (x,y), die auf dem Kreis mit dem Mittelpunkt \displaystyle (a,b) und dem Radius \displaystyle r liegen, können durch die Formel für den Abstand zwischen zwei Punkten beschrieben werden.

Die Gleichung eines Kreises:
\displaystyle (x – a)^2 + (y – b)^2 = r^2\,\mbox{.}

[Image]

Beispiel 6

  1. \displaystyle (x-1)^2 + (y-2)^2 = 9\quad ist die Gleichung eines Kreises mit dem Mittelpunkt \displaystyle (1,2) und dem Radius \displaystyle \sqrt{9} = 3.

[Image]

  1. \displaystyle x^2 + (y-1)^2 = 1\quad: Es gilt \displaystyle (x-0)^2 + (y-1)^2 = 1, also ist dies die Gleichung eines Kreises mit dem Mittelpunkt \displaystyle (0,1) und dem Radius \displaystyle \sqrt{1} = 1.

[Image]

  1. \displaystyle (x+1)^2 + (y-3)^2 = 5\quad: es ist \displaystyle (x-(-1))^2 + (y-3)^2 = 5, also ist dies Gleichung eines Kreises mit dem Mittelpunkt \displaystyle (-1,3) und dem Radius \displaystyle \sqrt{5} \approx 2\textrm{.}236.

[Image]

Beispiel 7

  1. Liegt der Punkt \displaystyle (1,2) auf dem Kreis \displaystyle (x-4)^2 +y^2=13?

    Wir kontrollieren, ob \displaystyle x=1 und \displaystyle y=2 die Gleichung des Kreises erfüllen:
    \displaystyle \begin{align*}

    \mbox{linke Seite } &= (1-4)^2+2^2\\ &= (-3)^2+2^2 = 9+4 = 13 = \mbox{Rechte Seite}\,\mbox{.} \end{align*}

    Nachdem der Punkt die Gleichung des Kreises erfüllt, liegt er auf dem Kreis.

    [Image]

  2. Bestimmen Sie die Gleichung für den Kreis, der den Mittelpunkt \displaystyle (3,4) hat und durch den Punkt \displaystyle (1,0) geht.

    Nachdem der Punkt \displaystyle (1,0) auf dem Kreis liegt, muss der Abstand zwischen diesem Punkt und dem Mittelpunkt \displaystyle (3,4) der Radius des Kreises sein. Also haben wir
    \displaystyle

    c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{}

    und die Gleichung des Kreises lautet:

    \displaystyle (x-3)^2 + (y-4)^2 = 20 \; \mbox{.}

    [Image]


Beispiel 8

Bestimme den Mittelpunkt und Radius des Kreises mit der Gleichung \displaystyle \ x^2 + y^2 – 2x + 4y + 1 = 0.


Wir wollen die Gleichung des Kreises auf die Form

\displaystyle (x – a)^2 + (y – b)^2 = r^2

bringen. Dann können wir den Mittelpunkt direkt als \displaystyle (a,b) ablesen, und den Radius als \displaystyle r.

Wir benutzen zuerst die quadratische Ergänzung für alle \displaystyle x-Terme auf der linken Seite

\displaystyle

\underline{x^2-2x\vphantom{(}} + y^2+4y + 1 = \underline{(x-1)^2-1^2} + y^2+4y + 1

(Wir haben nur die unterstrichenen Terme verändert)

Jetzt benutzen wir die quadratische Ergänzung für alle \displaystyle y-Terme

\displaystyle

(x-1)^2-1^2 + \underline{y^2+4y} + 1 = (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}

Die linke Seite ist also

\displaystyle (x-1)^2 + (y+2)^2-4

Wenn wir 4 zu beiden Seiten addieren, erhalten wir

\displaystyle (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}

Also hat der Kreis den Mittelpunkt \displaystyle (1,-2) und den Radius \displaystyle \sqrt{4}= 2.

[Image]



Noch Fragen zu diesem Kapitel? Dann schau nach im Kursforum (Du findest den Link in der Student Lounge) oder frag nach per Skype bei ombTutor My status My status

Keine Fragen mehr? Dann mache weiter mit den Übungen .


Tipps fürs Lernen

Diagnostische Prüfung und Schlussprüfung

Nachdem du mit der Theorie und den Übungen fertig bist, solltest Du die diagnostische Prüfung und die Schlussprüfung machen. Du findest die Links zu den Prüfungen in Deiner "Student Lounge".

Bedenken Sie folgendes:


Literaturhinweise

Für die, die tiefer in die Materie einsteigen wollen, sind hier einige Links angeführt:


Mehr über den Satz des Pythagoras in der Wikipedia

Lies mehr über Kreise auf Mathworld (engl.)


Nützliche Websites

Interaktive Experimente: Sinus und Cosinus im Einheitskreis (Flash)

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-TU-Berlin/index.php/4.1_Winkel_und_Kreise“