Solution 2.3:9b

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (14:11, 29 September 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
The points of intersection are those points on the curve which also lie on the
+
The points of intersection are those points on the curve which also lie on the ''x''-axis, i.e. they are those points which satisfy both the equation of the curve
-
<math>~x</math>
+
<math>y=x^{2}-5x+6</math> and the equation of the ''x''-axis <math>y=0</math>,
-
-axis, i.e. they are those points which satisfy both the equation of the curve
+
-
<math>y=x^{\text{2}}-\text{5}x+\text{6}</math>
+
-
and the equation of the
+
-
<math>~x</math>
+
-
-axis
+
-
<math>y=0</math>,
+
 +
{{Displayed math||<math>\left\{\begin{align}
 +
y&=x^{2}-5x+6\,,\\
 +
y&=0\,\textrm{.}
 +
\end{align}\right.</math>}}
-
<math>\left\{ \begin{matrix}
+
This system of equations gives directly that <math>y=0</math> and that <math>x</math> must satisfy the quadratic equation <math>x^{2}-5x+6=0\,</math>. By completing the square, we obtain that the left-hand side is
-
y=x^{\text{2}}-\text{5}x+\text{6} \\
+
-
y=0\quad \quad \quad \quad \\
+
-
\end{matrix} \right.</math>
+
 +
{{Displayed math||<math>\begin{align}
 +
x^{2} - 5x + 6 &= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \Bigl(\frac{5}{2}\Bigr)^{2} + 6\\[5pt]
 +
&= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \frac{25}{4} + \frac{24}{4}\\[5pt]
 +
&= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \frac{1}{4}
 +
\end{align}</math>}}
-
This system of equations gives directly that
+
and this gives that the equation has solutions <math>x=\tfrac{5}{2}\pm\tfrac{1}{2}</math>, i.e. <math>x=\tfrac{5}{2}-\tfrac{1}{2}=\tfrac{4}{2}=2</math> and <math>x=\tfrac{5}{2}+\tfrac{1}{2}=\tfrac{6}{2}=3</math>.
-
<math>y=0</math>
+
-
and that
+
-
<math>~x</math>
+
-
must satisfy the second-order equation
+
-
<math>x^{\text{2}}-\text{5}x+\text{6}=0</math>
+
-
. By completing the square, we obtain that the left-hand side is
+
 +
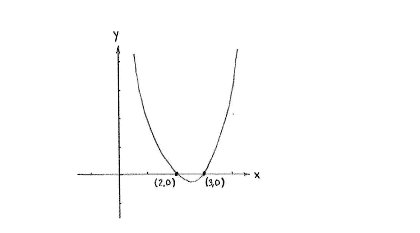
The intersection points are therefore (2,0) and (3,0).
-
<math>\begin{align}
 
-
& x^{\text{2}}-\text{5}x+\text{6}=\left( x-\frac{5}{2} \right)^{2}-\left( \frac{5}{2} \right)^{2}+6 \\
 
-
& =\left( x-\frac{5}{2} \right)^{2}-\frac{25}{4}+\frac{24}{4}=\left( x-\frac{5}{2} \right)^{2}-\frac{1}{4} \\
 
-
\end{align}</math>
 
-
 
+
<center>[[Image:2_3_9b-2(2).gif]]</center>
-
and this gives that the equation has solutions
+
-
 
+
-
<math>x=\frac{5}{2}\pm \frac{1}{2}</math>, i.e.
+
-
<math>x=\frac{5}{2}-\frac{1}{2}=\frac{4}{2}=2</math>
+
-
and
+
-
<math>x=\frac{5}{2}+\frac{1}{2}=\frac{6}{2}=3</math>.
+
-
 
+
-
The intersection points are therefore
+
-
<math>\left( 2 \right.,\left. 0 \right)</math>
+
-
and
+
-
<math>\left( 3 \right.,\left. 0 \right)</math>.
+
-
 
+
-
 
+
-
 
+
-
{{NAVCONTENT_START}}
+
-
<center> [[Image:2_3_9b-2(2).gif]] </center>
+
-
{{NAVCONTENT_STOP}}
+

Current revision

The points of intersection are those points on the curve which also lie on the x-axis, i.e. they are those points which satisfy both the equation of the curve \displaystyle y=x^{2}-5x+6 and the equation of the x-axis \displaystyle y=0,

\displaystyle \left\{\begin{align}

y&=x^{2}-5x+6\,,\\ y&=0\,\textrm{.} \end{align}\right.

This system of equations gives directly that \displaystyle y=0 and that \displaystyle x must satisfy the quadratic equation \displaystyle x^{2}-5x+6=0\,. By completing the square, we obtain that the left-hand side is

\displaystyle \begin{align}

x^{2} - 5x + 6 &= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \Bigl(\frac{5}{2}\Bigr)^{2} + 6\\[5pt] &= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \frac{25}{4} + \frac{24}{4}\\[5pt] &= \Bigl(x-\frac{5}{2}\Bigr)^{2} - \frac{1}{4} \end{align}

and this gives that the equation has solutions \displaystyle x=\tfrac{5}{2}\pm\tfrac{1}{2}, i.e. \displaystyle x=\tfrac{5}{2}-\tfrac{1}{2}=\tfrac{4}{2}=2 and \displaystyle x=\tfrac{5}{2}+\tfrac{1}{2}=\tfrac{6}{2}=3.

The intersection points are therefore (2,0) and (3,0).


Image:2_3_9b-2(2).gif
Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-ImperialCollege/index.php/Solution_2.3:9b"