Solution 2.2:5b

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (12:28, 24 September 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
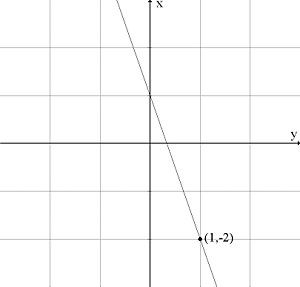
Because the straight line is to have a gradient of
+
Because the straight line is to have a slope of <math>-3</math>, its equation can be written as
-
<math>-3</math>, its equation can be written as
+
 +
{{Displayed math||<math>y=-3x+m\,,</math>}}
-
<math>y=-3x+m</math>
+
where ''m'' is a constant. If the line is also to pass through the point (''x'',''y'')&nbsp;= (1,-2), the point must satisfy the equation of the line,
 +
{{Displayed math||<math>-2=-3\cdot 1+m\,,</math>}}
-
where
+
which gives that <math>m=1</math>.
-
<math>m</math>
+
-
is a constant. If the line is also to pass through the point
+
-
<math>\left( x \right.,\left. y \right)=\left( 1 \right.,\left. -2 \right)</math>, the point
+
-
must satisfy the equation of the line
+
 +
The answer is thus that the equation of the line is <math>y=-3x+1</math>.
-
<math>-2=-3\centerdot 1+m</math>
 
- 
- 
-
which gives that
 
-
<math>m=1</math>.
 
- 
-
The answer is thus that the equation of the line is
 
-
<math>y=-3x+1</math>.
 
- 
- 
-
{{NAVCONTENT_START}}
 
[[Image:1_2_2_5_b_ss1.jpg|center|300px]]
[[Image:1_2_2_5_b_ss1.jpg|center|300px]]
-
{{NAVCONTENT_STOP}}
 

Current revision

Because the straight line is to have a slope of \displaystyle -3, its equation can be written as

\displaystyle y=-3x+m\,,

where m is a constant. If the line is also to pass through the point (x,y) = (1,-2), the point must satisfy the equation of the line,

\displaystyle -2=-3\cdot 1+m\,,

which gives that \displaystyle m=1.

The answer is thus that the equation of the line is \displaystyle y=-3x+1.


Retrieved from "http://wiki.sommarmatte.se/wikis/2009/bridgecourse1-ImperialCollege/index.php/Solution_2.2:5b"