From Förberedande kurs i matematik 1

Revision as of 10:58, 1 April 2008 (edit) Oskar (Talk | contribs) (Ny sida: {{NAVCONTENT_START}} <center> Bild:2_3_10c.gif </center> {{NAVCONTENT_STOP}}) ← Previous diff		Current revision (07:16, 30 September 2008) (edit) (undo) Tek (Talk | contribs) m
(6 intermediate revisions not shown.)
Line 1:		Line 1:
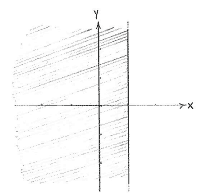
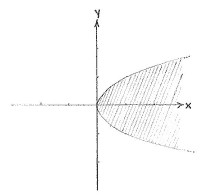
-	{{NAVCONTENT_START}}	+	The expression <math>1\ge x\ge y^{2}</math> means that we have a region which is defined by the two inequalities <math>1\ge x</math> and <math>x\ge y^{2}</math>. The first inequality gives us the region to the left of the line <math>x=1</math>. If the other inequality had been instead <math>y\ge x^{2}</math>, we would have a region above the parabola <math>y=x^{2}</math>, but in our case ''x'' and ''y'' have reversed roles, so the inequality <math>x\ge y^{2}</math> defines the same type of parabolic region, but with the ''x''- and ''y''-axes having changed place.
-	<center> [[Bild:2_3_10c.gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+
		+	{| align="center"
		+	|align="center"|[[Image:2_3_10_c1-1.gif|center]]
		+	|width="10px"|&nbsp;
		+	|align="center"|[[Image:2_3_10_c1-2.gif|center]]
		+	|-
		+	|align="center"|<small>The region 1&nbsp;≥&nbsp;''x''</small>
		+	||
		+	|align="center"|<small>The region ''x''&nbsp;≥&nbsp;''y''²</small>
		+	|}
		+
		+
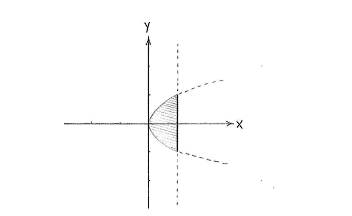
		+	Together, the inequalities define the region that is bordered on the left by the parabola and on the right by the line.
		+
		+
		+	{| align="center"
		+	|align="center"|[[Image:2_3_10_c2.gif|center]]
		+	|-
		+	|align="center"|<small>The region 1&nbsp;≥&nbsp;''x''&nbsp;≥&nbsp;''y''²</small>
		+	|}

---

Current revision

The expression \displaystyle 1\ge x\ge y^{2} means that we have a region which is defined by the two inequalities \displaystyle 1\ge x and \displaystyle x\ge y^{2}. The first inequality gives us the region to the left of the line \displaystyle x=1. If the other inequality had been instead \displaystyle y\ge x^{2}, we would have a region above the parabola \displaystyle y=x^{2}, but in our case x and y have reversed roles, so the inequality \displaystyle x\ge y^{2} defines the same type of parabolic region, but with the x- and y-axes having changed place.

The region 1 ≥ x		The region x ≥ y²

Together, the inequalities define the region that is bordered on the left by the parabola and on the right by the line.

The region 1 ≥ x ≥ y²