From Förberedande kurs i matematik 1

Revision as of 14:53, 31 March 2008 (edit) Lina (Talk | contribs) (Ny sida: {{NAVCONTENT_START}} <center> Bild:2_2_6b.gif </center> {{NAVCONTENT_STOP}}) ← Previous diff		Current revision (13:04, 24 September 2008) (edit) (undo) Tek (Talk | contribs) m
(4 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	Because the point of intersection lies on both lines, it must satisfy the equations of both lines
-	<center> [[Bild:2_2_6b.gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	{{Displayed math||<math>y=-x+5\qquad\text{and}\qquad x=0\,,</math>}}
		+
		+	where <math>x=0</math> is the equation of the ''y''-axis. Substituting the second equation, <math>x=0</math>, into the first equation gives <math>y=-0+5=5</math>. This means that the point of intersection is (0,5).
		+
		+
		+	<center>[[Image:2_2_6_b.gif]]</center>

---

Current revision

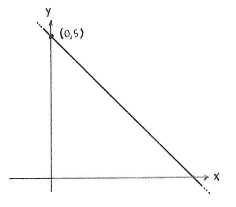
Because the point of intersection lies on both lines, it must satisfy the equations of both lines

\displaystyle y=-x+5\qquad\text{and}\qquad x=0\,,

where \displaystyle x=0 is the equation of the y-axis. Substituting the second equation, \displaystyle x=0, into the first equation gives \displaystyle y=-0+5=5. This means that the point of intersection is (0,5).